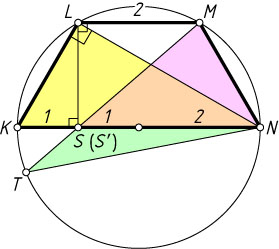
11. Около трапеции KLMN
описана окружность, причём основание KN
является её диаметром. Известно, что KN=4
, LM=2
. Хорда MT
пересекает диаметр KN
в точке S
, причём KS:SN=1:3
. Найдите площадь треугольника STN
.
Ответ. \frac{9\sqrt{3}}{14}
.
Решение. Пусть LS'
— высота трапеции KLMN
. Трапеция, вписанная в окружность, равнобедренная, поэтому
KS'=\frac{KN-LM}{2}=\frac{4-2}{2}=1=KS
(см. задачу 1921). Значит, точка S'
совпадает с S
.
Точка L
лежит на окружности с диаметром KN
, поэтому \angle KLN=90^{\circ}
, а LS
— высота прямоугольного треугольника KLN
, проведённая из вершины прямого угла. Значит, LS=\sqrt{KS\cdot SN}=\sqrt{3}
. По теореме Пифагора
SM=\sqrt{LS^{2}+LM^{2}}=\sqrt{3+4}=\sqrt{7},
поэтому
S_{\triangle MSN}=\frac{1}{2}SN\cdot LS=\frac{1}{2}\cdot3\cdot\sqrt{3}=\frac{3\sqrt{3}}{2}.
По теореме о произведении отрезков пересекающихся хорд (см. задачу 2627) TS\cdot SM=KS\cdot SN
, откуда
TS=\frac{KS\cdot SN}{SM}=\frac{1\cdot3}{\sqrt{7}}=\frac{3}{\sqrt{7}},
а так как
\frac{S_{\triangle STN}}{S_{\triangle MSN}}=\frac{TS}{SM}=\frac{\frac{3}{\sqrt{7}}}{\sqrt{7}}=\frac{3}{7}
(см. задачу 3000), то
S_{\triangle STN}=\frac{3}{7}S_{\triangle MSN}=\frac{3}{7}\cdot\frac{3\sqrt{3}}{2}=\frac{9\sqrt{3}}{14}.
