155. В остроугольном треугольнике ABC
угол A
равен 60^{\circ}
. Докажите, что биссектриса одного из углов, образованных высотами, проведёнными из вершин B
и C
, проходит через центр описанной окружности этого треугольника.
Указание. Точки C
и B
, центр описанной окружности и точка пересечения высот лежат на одной окружности.
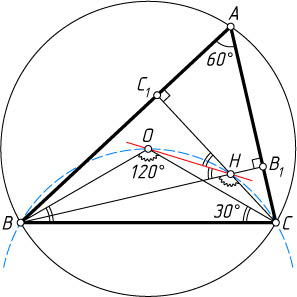
Решение. Первый способ. Для определённости будем считать, что AB\gt AC
. Пусть BB_{1}
и CC_{1}
— высоты (рис. 1), H
— точка пересечения высот, O
— центр описанной окружности.
Поскольку \angle COB=\angle CHB=120^{\circ}
, точки C
, H
, O
и B
лежат на одной окружности. Поэтому
\angle OHB=\angle OCB=\angle OBC=30^{\circ}=\frac{1}{2}\cdot60^{\circ}=\frac{1}{2}\angle BHC_{1}.
Следовательно, луч HO
— биссектриса угла BHC_{1}
.
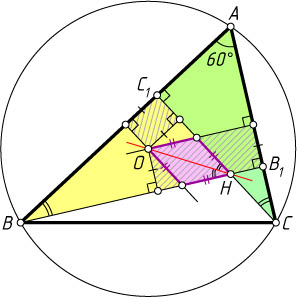
Второй способ. Точки H
и O
— противоположные вершины параллелограмма, образованного высотами BB_{1}
и CC_{1}
и серединными перпендикулярами к сторонам AB
и AC
(рис. 2). Расстояние от точки O
до прямой BB_{1}
равно
\left|AB_{1}-\frac{1}{2}AC\right|=\left|\frac{1}{2}AB-\frac{1}{2}AC\right|=\frac{1}{2}|AC-AB|
(поскольку в прямоугольном треугольнике ABB_{1}
катет, лежащий против угла в 30^{\circ}
, равен половине гипотенузы, т. е. AB_{1}=\frac{1}{2}AB
).
Тому же равно расстояние от точки O
до прямой CC_{1}
. Значит, этот параллелограмм — ромб. Следовательно, его диагональ — биссектриса угла между сторонами.
Третий способ. Предположим, что AB\gt AC
.
Докажем сначала, что общая биссектриса l
углов CHB_{1}
и BHC_{1}
перпендикулярна биссектрисе угла A
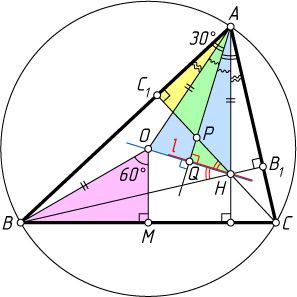
. Действительно, если биссектриса угла A
пересекает высоту CC_{1}
и прямую l
в точках P
и Q
соответственно (рис. 3), то
\angle PHQ=\frac{1}{2}\angle BHC_{1}=30^{\circ}=\angle PAC_{1},
значит, острые углы прямоугольного треугольника PAC_{1}
соответственно равны двум углам треугольника PHQ
. Следовательно, \angle HQP=90^{\circ}
, что и требовалось доказать.
Докажем теперь, что биссектриса угла A
перпендикулярна прямой, проходящей через точку H
пересечения высот треугольника ABC
и центр O
описанной окружности этого треугольника. Для этого воспользуемся двумя известными фактами: \angle OAB=\angle CAH
(см. задачу 20) и AH=2OM
, где M
— середина стороны BC
(см. задачу 1257).
Из первого следует, что биссектриса угла BAC
является также биссектрисой угла OAH
, а из второго — AH=2OM=BO=AO
(так как \angle MOB=60^{\circ}
), т. е. треугольник OAH
равнобедренный. Его биссектриса, проведённая из вершины A
, является высотой. Таким образом, проходящие через точку H
прямые HO
и l
перпендикулярны биссектрисе угла A
, значит, они совпадают. Отсюда следует утверждение задачи.
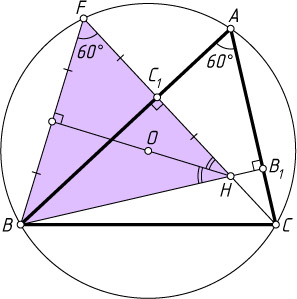
Четвёртый способ (Н.Волков). Продолжим высоту CC_{1}
до пересечения с описанной окружностью треугольника ABC
в точке F
(рис. 4). Тогда HC_{1}=C_{1}F
(см. задачу 4785). Высота BC_{1}
треугольника FBH
является его медианой, значит, треугольник HBF
равнобедренный, а так как \angle BFH=\angle BFC=\angle BAC=60^{\circ}
, то треугольник FBH
равносторонний. Точка O
лежит на серединном перпендикуляре к отрезку BF
, а в равностороннем треугольнике HBF
серединный перпендикуляр к его стороне BF
является биссектрисой угла BHF
. Отсюда следует утверждение задачи.
Примечание. Утверждение верно и для тупоугольного (прямоугольного) треугольника.
Автор: Погребняк В.
Источник: Турнир городов. — 1986-1987, VIII, весенний тур, младшие классы, основной вариант
Источник: Журнал «Квант». — 1987, № 10, с. 26, М1046
Источник: Задачник «Кванта». — М1046
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1987, заключительный тур, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 87.37



