162. Дан вписанный четырёхугольник ABCD
. Продолжения противоположных сторон AB
и CD
пересекаются в точке K
, сторон BC
и AD
— в точке L
. Докажите, что биссектрисы углов BKC
и BLA
перпендикулярны.
Указание. Угол между секущими равен полуразности высекаемых дуг. Угол между пересекающимися хордами равен полусумме высекаемых дуг (см. задачи 27 и 26).
Решение. Первый способ. Без ограничения общности будем считать, что точка B
лежит между A
и K
, а точка C
— между B
и L
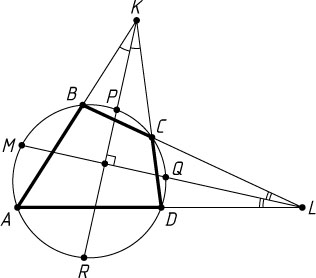
(см. рис.).
Пусть биссектриса угла BKC
пересекает окружность в точках P
и R
, а биссектриса угла BLA
— в точках Q
и M
. Тогда (см. задачу 27)
\smile AM-\smile DQ=\smile MB-\smile QC,~\smile DR-\smile CP=\smile AR-\smile BP,
или
\smile AM+\smile QC=\smile BM+\smile DQ,~\smile AR+\smile CP=\smile DR+\smile BP.
Сложив почленно последние два равенства, получим
\smile AR+\smile AM+\smile CP+\smile QC=\smile BM+\smile BP+\smile DR+\smile DQ.
Значит, каждая из этих сумм равна 180^{\circ}
. Следовательно, угол между хордами PR
и MQ
равен 90^{\circ}
.
Второй способ. Без ограничения общности будем считать, что точка B
лежит между A
и K
, а точка C
— между B
и L
(см. рис.).
Пусть биссектриса угла BKC
пересекает стороны BC
и AD
в точках окружность в точках E
и F
соответственно, а биссектриса угла пересекает стороны CD
и AB
в точках Q
и M
.
Поскольку четырёхугольник ABCD
вписанный,
\angle HBC=\angle ABC=\angle CDL=\angle CGL,
а так как LH
— биссектриса угла ALB
, то \angle BLH=\angle DLG
. Два угла треугольника BLH
соответственно равны двум углам треугольника DLG
, значит, и третьи углы также равны. Значит,
\angle KHG=\angle BHL=\angle DGL=\angle KGH,
поэтому треугольник GKH
равнобедренный. Его биссектриса, проведённая из вершины K
, является высотой, следовательно, KF\perp LH
.
Примечание. Обратное утверждение также верно: если биссектрисы углов, образованных прямыми, содержащими противоположные стороны выпуклого четырёхугольника, перпендикулярны, то около этого четырёхугольника можно описать окружность.(см. задачу 4131).
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 148, с. 45
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 107 (фрагмент), с. 105
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 8, с. 75
Источник: Журнал «Квант». — 1983, № 8, с. 36, задача 27
