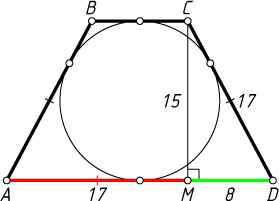
324. Около окружности с диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите основания трапеции.
Ответ. 9 и 25.
Указание. См. задачи 1921 и 1912.
Решение. Пусть M
— основание высоты, проведённой из вершины C
меньшего основания BC
трапеции ABCD
к большему основанию AD
. Тогда
MD=\sqrt{CD^{2}-CM^{2}}=8.
По свойству описанного четырёхугольника (см. задачу 310)
AD+BC=AB+CD=2CD=34.
По свойству равнобедренной трапеции (см. задачи 1921 и 1912)
AM=\frac{AD+BC}{2}=17,~DM=\frac{AD-BC}{2}=8.
Отсюда находим, что AD=25
, BC=9
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.007. с. 159
