10216. С помощью циркуля и линейки постройте радикальную ось двух данных окружностей.
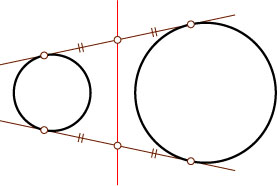
Решение. 1. Пусть данные окружности расположены одна вне другой (рис. 1). Тогда их радикальная ось — прямая проходящая через середины общих касательных (см. задачу 6122).
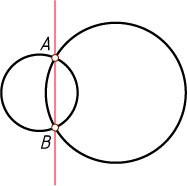
2. Пусть окружности пересекаются в точках A
и B
(рис. 2). Тогда их радикальная ось — прямая AB
(см. задачу 6392).
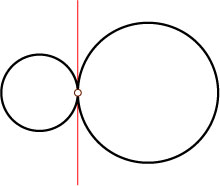
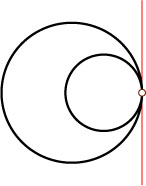
3. Пусть окружности касаются (рис. 3 и 4). Тогда их радикальная ось — общая касательная, проведённая через точку касания (см. задачу 6391).
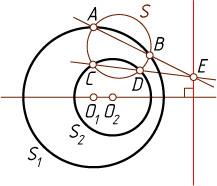
4. Пусть окружность S_{2}
с центром O_{2}
расположена внутри окружности S_{1}
с центром O_{1}
, причём точки O_{1}
и O_{2}
различны (рис. 5). Проведём произвольную окружность S
с центром, не лежащем на прямой O_{1}O_{2}
, и пересекающую окружность S_{1}
в точках A
и B
, а окружность S_{2}
— в точках C
и D
. Тогда прямая AB
— радикальная ось окружностей S
и S_{1}
, а прямая CD
— радикальная ось окружностей S
и S_{2}
.
Пусть прямые AB
и CD
пересекаются в точке E
. Тогда E
— радикальный центр окружностей S
, S_{1}
и S_{2}
(см. задачу 6393). Следовательно, радикальная ось окружностей S_{1}
и S_{2}
— прямая, проходящая через точку E
перпендикулярно линии центров O_{1}O_{2}
окружностей S_{1}
и S_{2}
.
5. Для концентрических окружностей задача не имеет решения.