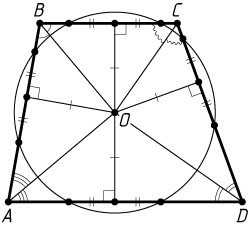
10511. Окружность с центром O
высекает на всех сторонах трапеции ABCD
равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются одной точке.
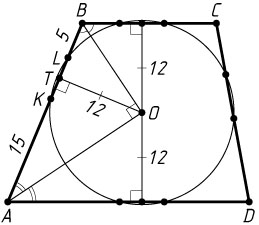
б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB
в точках K
и L
так, что AK=15
, KL=6
, LB=5
.
Ответ. 24
.
Решение. а) Равные хорды равноудалены от центра окружности (см. задачу 1673), поэтому точка O
равноудалена от всех сторон трапеции. Следовательно, O
— точка пересечения биссектрис всех углов трапеции (см. задачу 1138), т. е. эти биссектрисы пересекаются в точке O
.
б) Пусть T
— основание перпендикуляра, опущенного из точки O
на боковую сторону AB
. Тогда T
— середина хорды KL
. Треугольник AOB
прямоугольный, так как лучи AO
и BO
— биссектрисы углов, сумма которых равна 180^{\circ}
. Значит, OT
— высота прямоугольного треугольника, проведённая из вершины прямого угла, поэтому (см. задачу 2728)
OT=\sqrt{AT\cdot BT}=\sqrt{(AK+KT)(TL+LB)}=\sqrt{(15+3)(3+5)}=12.
Расстояния от точки O
до оснований трапеции также равны 12, следовательно, высота трапеции равна 24.
Источник: ЕГЭ. — 2018, 1 июня

