10875. Пусть AA_{1}
и BB_{1}
— высоты остроугольного неравнобедренного треугольника ABC
, \omega
и \omega_{1}
— окружности, описанные около треугольников ABC
и A_{1}B_{1}C
соответственно, P
— вторая точка их пересечения, S
— точка пересечения прямых A_{1}B_{1}
и AB
. Докажите, что точки C
, P
и S
лежат на одной прямой.
Решение. Точки A_{1}
и B_{1}
лежат на окружности с диаметром AB
(см. задачу 1691). Обозначим её \omega_{2}
. Прямые CP
, A_{1}B_{1}
, AB
— радикальные оси пар окружностей \omega
и \omega_{1}
, \omega_{1}
и \omega_{2}
, \omega
и \omega_{2}
соответственно (см. задачу 6392). Эти прямые пересекаются в точке S
— радикальном центре окружностей \omega
, \omega_{1}
и \omega_{2}
(см. задачу 6393). Следовательно, точка S
лежит на прямой CP
.
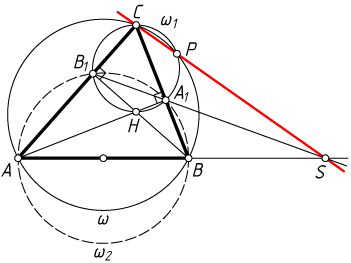
Примечание. 1. Это утверждение верно и для тупоугольного неравнобедренного треугольника.
2. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Источник: Журнал «Квант». — 2014, № 1, с. 44
