10881. Пусть AA_{1}
, BB_{1}
и CC_{1}
— высоты неравнобедренного остроугольного треугольника ABC
, P
— вторая точка пересечения описанных окружностей треугольников ABC
и A_{1}B_{1}C
, Касательные, проведённые к описанной окружности треугольника ABC
в точках A
и B
, пересекаются в точке Z
. Докажите, что прямые AP
, BC
и ZC_{1}
пересекаются в одной точке.
Указание. См. задачи 10874, 533, 700.
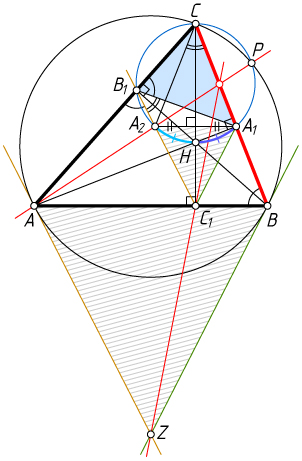
Решение. Пусть A_{2}
— точка, симметричная точке A_{1}
относительно высоты CC_{1}
. Точка A_{2}
лежит на прямой AP
(см. задачу 10874(в)), на окружности, описанной около треугольника A_{1}B_{1}C_{1}
, а также на прямой B_{1}C_{1}
, так как
\angle A_{1}B_{1}C_{1}=180^{\circ}-\angle AB_{1}C_{1}-\angle CB_{1}A_{1}=180^{\circ}-2\angle ABC,
\angle A_{1}B_{1}A_{2}=\angle A_{1}CA_{2}=2\angle A_{1}CH=2(90^{\circ}-\angle ABC)=180^{\circ}-2\angle ABC=\angle A_{1}B_{1}C_{1}
(см. задачу 533).
Кроме того, B_{1}C_{1}\parallel AZ
и A_{1}C_{1}\parallel BZ
(см. задачу 700), а так как прямые A_{2}A_{1}
и AB
перпендикулярны высоте CC_{1}
, эти прямые также параллельны. Таким образом, у равнобедренных треугольников AZB
и A_{2}C_{1}A_{1}
соответствующие стороны параллельны. Следовательно, эти треугольники гомотетичны, причём центр гомотетии лежит на пересечении прямых AA_{2}
, BA_{1}
и ZC_{1}
. Следовательно, прямые AP
, BC
и ZC_{1}
пересекаются в одной точке.
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Блинков Ю. А.
Источник: Журнал «Квант». — 2014, № 1, с. 46
