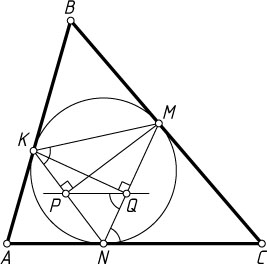
700. Точки касания вписанной в треугольник окружности соединены отрезками и в полученном треугольнике проведены высоты. Докажите, что прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника.
Указание. Примените теорему об угле между касательной и хордой (см. задачу 87) или теорему Нагеля (см. задачу 480).
Решение. Пусть M
, N
и K
— точки касания окружности, вписанной в треугольник ABC
, со сторонами BC
, AC
и AB
соответственно; MP
и KQ
— высоты треугольника MNK
.
Первый способ. Из теоремы об угле между касательной и хордой следует, что \angle MNC=\angle MKN
, а так как \angle MKN=\angle PQN
(см. задачу 141), то \angle MNC=\angle PQN
. Следовательно, PQ\parallel AC
. Аналогично для остальных сторон треугольника с вершинами в основаниях высот треугольника MKN
.
Второй способ. Вписанная окружность треугольника ABC
— это описанная окружность треугольника MNK
. Пусть O
— её центр. Тогда ON\perp AC
и ON\perp PQ
(см. задачу 480). Следовательно, PQ\parallel AC
. Аналогично для остальных сторон треугольника с вершинами в основаниях высот треугольника MKN
.
Примечание. Заметим, что ABC
— тангенциальный треугольник треугольника MNK
, т. е. треугольник, образованный касательными к описанной окружности треугольника MNK
, проведёнными в точках касания. Из условия следует, что треугольник MNK
остроугольный (см. задачу 1303), однако верно следующее утверждение.
Стороны тангенциального треугольника ABC
любого треугольника MNK
соответственно параллельны сторонам ортотреугольника треугольника MNK
(см. задачу 13011).
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 93, с. 39
Источник: Физико-математическая олимпиада МИРЭА. — 9 кл.
