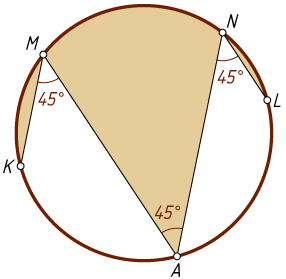
10886. Вершины ломаной KMANL
лежат на окружности и \angle KMA=\angle MAN=\angle ANL=45^{\circ}
(см. рис.). Докажите, что площадь закрашенной части равна половине площади круга.
Решение. Проведём отрезок KL
(рис. 1). Он является диаметром окружности, так как сумма угловых величин дуг KA
и LA
равна 180^{\circ}
.
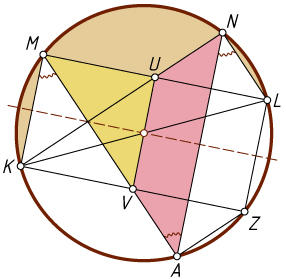
Первый способ. Проведём через точку L
прямую, параллельную MK
, до пересечения с окружностью в точке Z
. Тогда ML=KZ
как хорды, отсекающие равные дуги, а так как KL
— диаметр окружности, то углы KML
и KZL
прямые, поэтому KMLZ
— прямоугольник.
Пусть U
— точка пересечения KN
и ML
, V
— точка пересечения MA
и KZ
. Окружность симметрична относительно диаметра, параллельного ML
. При этой симметрии хорда KN
переходит в хорду MA
, а хорда ML
— в хорду KZ
, поэтому точка U
переходит в V
. Тогда UV\parallel LZ
.
Проведём отрезок AZ
. Заметим, что равны сегменты, ограниченные хордами MK
и LZ
, NL
и AZ
, равны трапеции UVAN
и LZAN
, равны треугольники MUV
и VKM
, а также — криволинейные треугольники MUN
и KVA
. Значит, для каждого «куска» закрашенной части найдётся симметричный ему незакрашенный «кусок». Отсюда следует утверждение задачи.
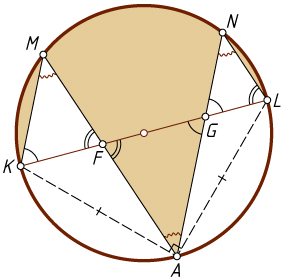
Второй способ. Пусть KL
пересекает AM
и AN
в точках F
и G
соответственно (рис. 2). Тогда утверждение задачи равносильно равенству
S_{\triangle KMF}+S_{\triangle LNG}=S_{\triangle FAG}.
Дуги AK
и AL
равны (на них опираются равные вписанные углы), а KL
— диаметр окружности, значит, треугольник KAL
— прямоугольный и равнобедренный. Тогда
FG^{2}=KF^{2}+LG^{2}
(см. задачу 10124). Заметим также, что треугольники FMK
и LNG
подобны треугольнику FAG
(по двум углам) с коэффициентами k_{1}=\frac{KF}{FG}
и k_{2}=\frac{LG}{FG}
соответственно. Тогда
\frac{S_{\triangle KMF}}{S_{\triangle FAG}}=k_{1}^{2}=\frac{KF^{2}}{FG^{2}}~\mbox{и}~\frac{S_{\triangle LNG}}{S_{\triangle FAG}}=k_{2}^{2}=\frac{LG^{2}}{FG^{2}}.
Складывая эти равенства почленно, получим, что
\frac{S_{\triangle KMF}+S_{\triangle LNG}}{S_{\triangle FAG}}=\frac{KF^{2}+LG^{2}}{FG^{2}}=1.
Отсюда следует утверждение задачи.
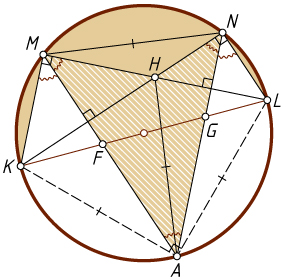
Третий способ. Пусть KL
пересекает AM
и AN
в точках F
и G
соответственно (рис. 3). Тогда утверждение задачи равносильно равенству
S_{\triangle KMF}+S_{\triangle LNG}=S_{\triangle FAG}.
Прибавив к обеим частям этого равенства площади треугольников AFK
и AGL
, получим, что оно равносильно равенству
S_{\triangle KMA}+S_{\triangle LNA}=S_{\triangle KAL}.
Пусть H
— точка пересечения KN
и ML
. Угол KMH
прямой, так как KL
— диаметр окружности. Тогда
\angle HMA=\angle KMA=45^{\circ}~\mbox{и}~\angle MKH=\angle MAN=45^{\circ},
поэтому AM\perp KH
. Значит, при симметрии относительно прямой AM
точка K
перейдёт в H
. Аналогично, при симметрии относительно прямой AN
точка L
перейдёт в H
. Следовательно,
S_{\triangle KMA}+S_{\triangle LNA}=S_{\triangle HMA}+S_{\triangle HNA}=S_{AMHN}.
В невыпуклом четырёхугольнике AMHN
три угла по 45^{\circ}
, значит, MN=AH
и MN\perp AH
(см. задачу 4272). Следовательно (см. задачу 3018),
S_{AMHN}=\frac{1}{2}AH\cdot MN=\frac{1}{2}AH^{2}=\frac{1}{2}AK\cdot AL=S_{\triangle KAL}.
Примечание. См. статью А.Блинкова и Ю.Блинкова «Угол в квадрате», Квант, 2014, N4, с.34-37.
Источник: Произволов В. В. Задачи на вырост. — М.: МИРОС, 1995. — № 6, с. 56
Источник: Журнал «Квант». — 2014, № 4, с. 35



