10906. Вписанная в трапецию окружность пересекает её диагонали в точках A
, B
, C
, D
(см. рис.). Докажите, что сумма длин дуг \smile BA+\smile DC
больше суммы длин дуг \smile AD+\smile CB
.
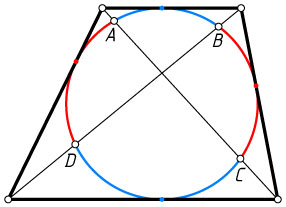
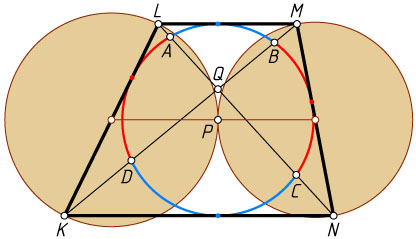
Решение. Пусть Q
— точка пересечения диагоналей KM
и LN
трапеции KLMN
с основаниями KN
и LM
, а вписанная в трапецию окружность пересекает отрезки QL
, QM
, QN
и QK
в точках A
, B
, C
И D
соответственно. Поскольку трапеция описанная, окружности с диаметрами KL
и MN
касаются в некоторой точке P
(см. задачу 728). Точка Q
не может совпасть с P
, так как точка P
лежит на средней линии трапеции, и поэтому равноудалена от прямых KN
и LM
. Очевидно, что точка не может оказаться внутри каждой из окружностей с диаметрами KM
и LN
. Значит, Q
лежит вне этих окружностей. Тогда углы AQD
и BQC
острые (см. задачу 1772), поэтому (см. задачу 26)
\smile AD+\smile CB=2\angle AQD=2(\angle AQD+\angle BQC)\lt2\cdot90^{\circ}=180^{\circ}.
Значит,
\smile BA+\smile DC=360^{\circ}-(\smile AD+\smile CB)\gt180^{\circ}.
Следовательно,
\smile BA+\smile DC\gt\smile AD+\smile CB.
Источник: Журнал «Квант». — 2018, № 12, с. 44
Источник: Межрегиональная олимпиада школьников на базе ведомственных образовательных программ. — 2018, № 9

