12401. В угол вписаны две непересекающиеся окружности. Одной стороны угла они касаются в точках K
и L
, другой — в точках M
и N
(см. рисунок), C
— середина отрезка KL
, A
и B
— точки пересечения отрезков CM
и CN
с окружностями. Докажите, что:
а) точки A
, B
, M
и N
лежат на одной окружности;
б) точки A
, B
, K
и L
лежат на одной окружности.
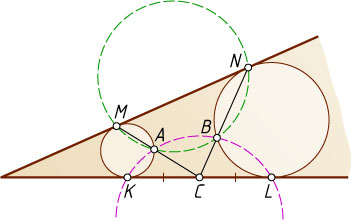
Решение. а) По теореме о касательной и секущей (см. задачу 93)
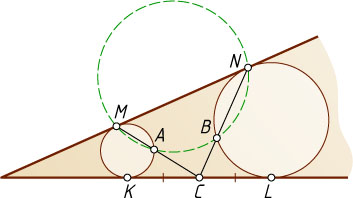
CA\cdot CM=CK^{2}=CL^{2}=CB\cdot CN.
Следовательно, четырёхугольник MABN
вписанный (см. задачу 114).
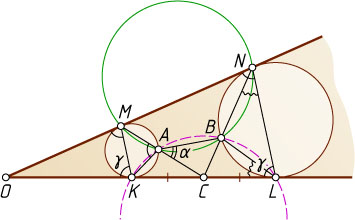
б) Пусть O
— вершина данного угла. Центр окружности, вписанной в угол, лежит на биссектрисе угла (см. задачу 1724), а угол симметричен относительно его биссектрисы, поэтому MNLK
— равнобедренная трапеция. Обозначим \angle BAC=\alpha
, \angle OLN=\angle OKM=\gamma
. Тогда из теоремы об угле между касательной и хордой получаем
\angle KAC=180^{\circ}-\angle KAM=180^{\circ}-\angle OKM=180^{\circ}-\gamma,
\angle KAB=\angle KAC+\angle BAC=180^{\circ}-\gamma+\alpha.
С другой стороны,
\angle KLB=\angle BNL=\angle ONL-\angle MNB=\angle ONL-(180^{\circ}-\angle BAM)=
=\angle ONL-\angle BAC=\gamma-\alpha.
Значит,
\angle KLB+\angle KAB=(180^{\circ}-\gamma+\alpha)+(\gamma-\alpha)=180^{\circ}.
Тогда четырёхугольник ABLK
вписанный (см. задачу 49). Следовательно, точки A
, B
, K
и L
лежат на одной окружности.
Источник: Олимпиада «Курчатов». — 2014-2015, финальный этап, задача 4, 10-11 класс


