12547. Точки P_{1}
и P_{2}
разбивают сторону BC
треугольника ABC
на три равные части (см. рис.), точки Q_{1}
и Q_{2}
разбивают сторону CA
на три равные части, точки R_{1}
и R_{2}
разбивают сторону AB
на три равные части. Докажите, что:
а) треугольники P_{1}Q_{1}R_{1}
и P_{2}Q_{2}R_{2}
равны;
б) S_{\triangle P_{1}Q_{1}R_{1}}=\frac{1}{3}S_{\triangle ABC}
;
в) стороны треугольников P_{1}Q_{1}R_{1}
и P_{2}Q_{2}R_{2}
разбивают друг друга на три равные части;
г) если M_{1}
— середина стороны AB
, то точки C
, S
, T
и M_{1}
(см. рис.) лежат на одной прямой.
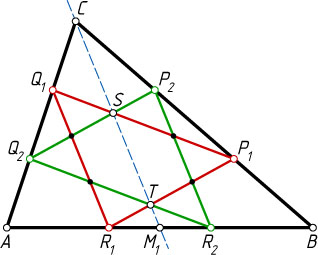
Решение. а) Треугольник Q_{1}CP_{2}
подобен треугольнику ABC
с коэффициентом \frac{1}{3}
, поэтому
Q_{1}P_{2}=\frac{1}{3}AB=R_{1}R_{2}.
При этом Q_{1}P_{2}\parallel R_{1}R_{2}
, значит, R_{1}Q_{1}P_{2}R_{2}
— параллелограмм. Тогда Q_{1}R_{1}=P_{2}R_{2}
. Аналогично, P_{1}Q_{1}=R_{2}Q_{2}
и P_{1}R_{1}=P_{2}Q_{2}
. Следовательно, треугольники P_{1}Q_{1}R_{1}
и P_{2}Q_{2}R_{2}
равны по трём сторонам.
б) Поскольку (см. задачу 3007)
S_{\triangle Q_{1}AR_{1}}=\frac{AQ_{1}}{AC}\cdot\frac{AR_{1}}{AB}S_{\triangle ABC}=\frac{2}{3}\cdot\frac{1}{3}S_{\triangle ABC}=\frac{2}{9}S_{\triangle ABC}
и аналогично,
S_{\triangle P_{1}BR_{1}}=\frac{2}{9}S_{\triangle ABC},~S_{\triangle P_{1}CQ_{1}}=\frac{2}{9}S_{\triangle ABC},
то
S_{\triangle P_{1}Q_{1}R_{1}}=S_{\triangle ABC}-S_{\triangle Q_{1}AR_{1}}-S_{\triangle P_{1}BR_{1}}-S_{\triangle P_{1}CQ_{1}}=
=S_{\triangle ABC}-3\cdot\frac{2}{9}S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}.
в) Поскольку S
— точка пересечения медиан P_{1}Q_{1}
и Q_{2}P_{2}
треугольника CP_{1}Q_{2}
, то Q_{1}S=\frac{1}{3}P_{1}Q_{1}
. Аналогично из треугольника Q_{1}DR_{2}
получаем, что P_{1}V=\frac{1}{3}P_{1}Q_{1}
. Значит,
SV=P_{1}Q_{1}-2\cdot\frac{1}{3}P_{1}Q_{1}=\frac{1}{3}P_{1}Q_{1},
т. е. P_{1}V=SV=SQ_{1}
. Остальное аналогично.
г) Поскольку CM_{1}
— медиана треугольника ABC
, а P_{2}Q_{1}\parallel AB\parallel P_{1}Q_{2}
, то прямая CM_{1}
проходит через середины отрезков P_{2}Q_{1}
и P_{1}Q_{2}
(см. задачу 2607). Поскольку S
и T
— точки пересечения диагоналей трапеций P_{1}P_{2}Q_{1}Q_{2}
и BP_{1}Q_{2}A
соответственно, а прямая CM_{1}
проходит через середины их оснований P_{2}Q_{1}
, P_{1}Q_{2}
и AB
, то на этой прямой лежат точки S
и T
пересечения диагоналей этих трапеций (см. задачу 1513).
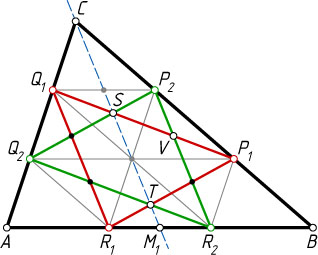
Источник: Журнал «Crux Mathematicorum». — 1978, № 8, задача 320, с. 238

