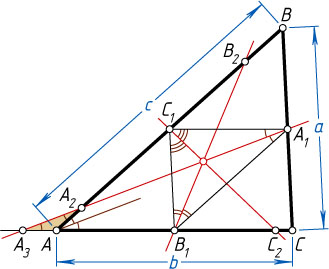
13190. В треугольнике ABC
точки A_{1}
, B_{1}
, C_{1}
— середины сторон BC
, AC
, AB
соответственно. Точки A_{2}
, B_{2}
, C_{2}
— середины ломаных BAC
, ABC
, ACB
соответственно (точка называется серединой ломаной если принадлежит ломаной и делит её на две ломаных равной длины). Докажите, что прямые A_{1}A_{2}
, B_{1}B_{2}
, C_{1}C_{2}
проходят через одну точку.
Решение. Пусть BC=a
, AC=b
, AB=c
. Не умаляя общности, считаем, что a\leqslant b\leqslant c
. Тогда точка A_{2}
лежит на отрезке AB
, причём AA_{2}+b=c-AA_{2}
, откуда AA_{2}=\frac{c-b}{2}
. Аналогично получаем, что точка B_{2}
лежит на отрезке AB
, причём BB_{2}=\frac{c-a}{2}
, а точка C_{2}
лежит на отрезке AC
, причём CC_{2}=\frac{b-a}{2}
.
Первый способ. Пусть A_{3}
— точка пересечения прямых AC
и A_{1}A_{2}
Обозначим AA_{3}=x
, причём отрезок AA_{3}
будем считать положительно направленным, а отрезок AC
— отрицательно направленным. Тогда по теореме Менелая для треугольника ABC
и прямой A_{1}A_{2}
получим, что
-1=\frac{AA_{2}}{A_{2}B}\cdot\frac{BA_{1}}{A_{1}C}\cdot\frac{CA_{3}}{A_{3}A}=\frac{\frac{c-b}{2}}{\frac{b+c}{2}}\cdot\frac{\frac{a}{2}}{\frac{a}{2}}\cdot\frac{b+x}{(-x)}=-\frac{(c-b)(b+x)}{(b+c)x},
откуда после очевидных упрощений находим, что
AA_{3}=x=\frac{c-b}{2}=AA_{2}.
Поскольку треугольник AA_{2}A_{3}
равнобедренный, его основание A_{2}A_{3}
параллельно биссектрисе внешнего угла при вершине A
(см. задачу 1174), т. е. параллельно биссектрисе внутреннего угла треугольника ABC
при вершине A
. Следовательно, луч A_{1}A_{2}
— биссектриса угла B_{1}A_{1}C_{1}
. Аналогично, лучи B_{1}B_{2}
и C_{1}C_{2}
— биссектрисы углов треугольника B_{1}A_{1}C_{1}
, и значит, все три прямые A_{1}A_{2}
, B_{1}B_{2}
, C_{1}C_{2}
пересекаются в одной точке — центре вписанной окружности треугольника B_{1}A_{1}C_{1}
.
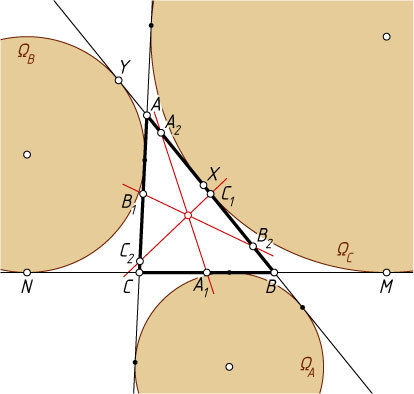
Второй способ. Пусть \Omega_{A}
, \Omega_{B}
, \Omega_{C}
— вневписанные окружности треугольника ABC
, касающиеся сторон BC
, AC
и AB
соответственно, X
и Y
— точки касания с прямой AB
окружностей \Omega_{C}
и \Omega_{B}
соответственно, M
и N
— точки касания с прямой BC
окружностей \Omega_{C}
и \Omega_{B}
соответственно, p
— полупериметр треугольника ABC
. Тогда (см. задачу 1750)
A_{2}Y=A_{2}A+AY=\frac{c-b}{2}+p-c=\frac{c-b}{2}+\frac{a+b-c}{2}=\frac{a}{2},
A_{2}X=|BA_{2}-BX|=|BA_{2}-BM|=\left|\frac{b+c}{2}-(p-a)\right|=\frac{a}{2}=A_{2}Y.
Значит, точка A_{2}
лежит на радикальной оси окружностей \Omega_{C}
и \Omega_{B}
, а так как
A_{1}M=A_{1}B+BM=\frac{a}{2}+p-a=p-\frac{a}{2},
A_{1}N=A_{1}C+CN=\frac{a}{2}+p-a=p-\frac{a}{2},
то A_{1}M=A_{1}N
. Значит, точка A_{1}
тоже лежит на радикальной оси этих окружностей. Следовательно, прямая A_{1}A_{2}
— радикальная ось окружностей \Omega_{C}
и \Omega_{B}
. Аналогично доказывается, что прямая B_{1}B_{2}
— радикальная ось окружностей \Omega_{A}
и \Omega_{C}
, а прямая C_{1}C_{2}
— радикальная ось окружностей \Omega_{A}
и \Omega_{B}
. Следовательно, прямые A_{1}A_{2}
, B_{1}B_{2}
и C_{1}C_{2}
пересекаются в одной точке — радикальном центре окружностей \Omega_{A}
, \Omega_{B}
, \Omega_{C}
(см. задачу 6393)
Источник: Олимпиада «Высшая проба» (математическая олимпиада ВШЭ). — 2020, заключительный этап, задача 3, 9 класс

