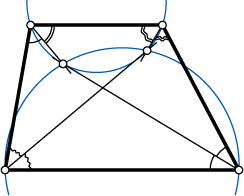
13419. Докажите, что точки пересечения биссектрис противоположных углов трапеции вместе с концами каждого из её оснований лежат на одной окружности. Для определённости будем считать, что точки расположены так, как показано на рисунке.
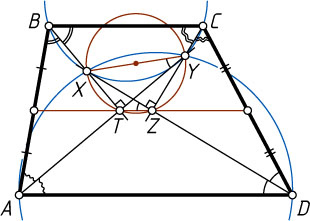
Решение. Пусть биссектрисы противоположных углов B
и D
трапеции ABCD
с основаниями AD
и BC
пересекаются в точке X
, а биссектрисы углов A
и C
— в точке Y
. Кроме того, пусть биссектрисы углов A
и B
пересекаются в точке T
, а биссектрисы углов C
и D
— в точке Z
.
Точки T
и Z
лежат на средней линии трапеции (см. задачу 1268), поэтому TZ\parallel AD
, а так как биссектрисы углов при боковой стороне трапеции перпендикулярны (см. задачу 313), то из точек T
и Z
отрезок XY
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром XY
.
Вписанные в эту окружность углы XYT
и XZT
опираются на одну и ту же дугу, поэтому они равны. Значит,
\angle XYA=\angle XYT=\angle XZT=\angle XDA.
Отрезок AX
виден из точек Y
и D
, лежащих по одну сторону от прямой AX
, под равными углами, следовательно, точки X
, Y
, A
и D
лежат на одной окружности (см. задачу 12). Аналогично, для точек X
, Y
, B
и C
. Что и требовалось доказать.
Автор: Кузнецов А. С.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2022, второй тур, задача 3, 9 класс

