13738. Дан прямоугольник ABCD
. Точка P
лежит на прямой CD
, точки M
и N
— середины сторон AD
и BC
соответственно, прямые PM
и AC
пересекаются в точке Q
. Докажите, что луч NM
— биссектриса угла, образованного пересечением прямых PN
и QN
.
Решение. Пусть O
— центр прямоугольника ABCD
, а R
— точка пересечения QN
и CD
. Тогда продолжение медианы QO
треугольника MQN
пересекает отрезок PR
в его середине C
(см. задачи 2607 или 1523). Высота NC
треугольника PNR
является его медианой, значит, этот треугольник равнобедренный, и NC
— биссектриса его угла PNR
.
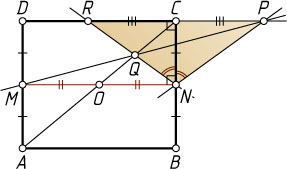
Случай 1. Точки P
и D
лежат по разные стороны от прямой BC
. Тогда луч NM
, параллельный основанию PR
равнобедренного треугольника PNR
, перпендикулярен CN
. Следовательно, NM
— биссектриса внешнего угла при вершине N
этого треугольника (см. задачу 1174), т. е. биссектриса угла, смежного с углом PNQ
.
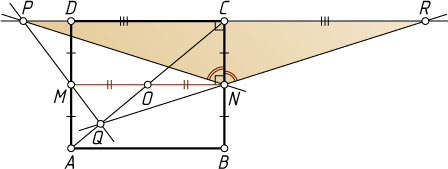
Случай 2. Точки P
и D
лежат по одну сторону от прямой BC
. Тогда луч NM
, параллельный основанию PR
равнобедренного треугольника PNR
, — биссектриса угла PNR
(см. задачу 1174), т. е. угла PNQ
.