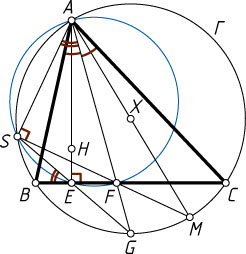
13986. Около остроугольного треугольника ABC
с высотой AE
и ортоцентром H
описана окружность \Gamma
. Биссектриса угла BAC
пересекает окружность \Gamma
в точке G
, а сторону BC
— в точке F
. Прямая GE
вторично пересекает окружность в точке S
, а прямая SF
вторично пересекает окружность \Gamma
в точке M
. Точка X
— середина отрезка AM
. Докажите, что
\overrightarrow{AH}=\overrightarrow{XB}+\overrightarrow{XC}.
Решение. Рассмотрим случай изображённый на рисунке.
По теореме об угле между пересекающимися хордами (см. задачу 26)
\angle BES=\frac{1}{2}\smile SB+\frac{1}{2}\smile GC=\angle SAB+\angle GAC=
=\angle SAB+\angle BAG=\angle SAG=\angle SAF,
поэтому
\angle SEF=180^{\circ}-\angle BES=180^{\circ}-\angle SAF.
Значит, AFES
— вписанный четырёхугольник. Тогда
\angle ASM=\angle ASF=\angle AEF=90^{\circ}.
Следовательно, AM
— диаметр окружности \Gamma
, а его середина X
— центр этой окружности.
Тогда (см. задачу 4516)
\overrightarrow{AH}=\overrightarrow{XH}-\overrightarrow{XA}=(\overrightarrow{XA}+\overrightarrow{XB}+\overrightarrow{XC})-\overrightarrow{XA}=\overrightarrow{XB}+\overrightarrow{XC}.
Что и требовалось доказать.
Аналогично для любого другого случая.
Примечание. 1. Разбора случаев можно избежать, если рассматривать ориентированные углы (см. задачу 873).
2. Утверждение верно для любого треугольника, не обязательно для остроугольного.
Источник: Журнал «Crux Mathematicorum». — 2018, № 2, задача 4216, с. 78
Источник: Иранские математические олимпиады. — 2015
