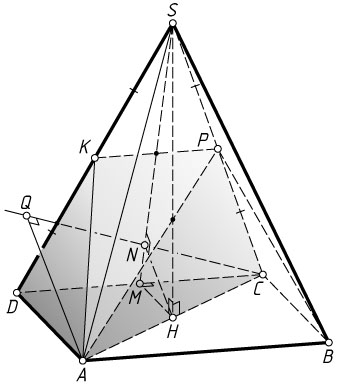
14089. В правильной четырёхугольной пирамиде SABCD
сторона основания AD
равна 10, высота SH
равна 12. Точка K
— середина бокового ребра SD
. Плоскость AKB
пересекает боковое ребро SC
в точке P
.
а) Докажите, что площадь четырёхугольника CDKP
составляет \frac{3}{4}
площади треугольника SCD
.
б) Найдите объём пирамиды ACDKP
.
Ответ. 150
.
Решение. а) Плоскости AKB
и CSD
проходят через параллельные прямые AB
и CD
соответственно и пересекаются по прямой KP
, значит, KP\parallel CD
(см. задачу 8004). Тогда KP
— средняя линия треугольника CSD
, поэтому S_{\triangle PSK}=\frac{1}{4}S_{\triangle CSD}
. Следовательно, S_{CDKP}=\frac{3}{4}S_{\triangle CSD}
. Что и требовалось доказать.
б) Пусть M
— середина ребра CD
. Тогда HM
— средняя линия треугольника ACD
, поэтому HM=\frac{1}{2}AD=5
и HM\perp CD
. По теореме о трёх перпендикулярах SM\perp CD
, т. е. SM
— высота треугольника CSD
. По теореме Пифагора
SM=\sqrt{SH^{2}+HM^{2}}=\sqrt{12^{2}+5^{2}}=13.
Значит,
S_{\triangle CSD}=\frac{1}{2}CD\cdot SM=5\cdot13=65,~S_{CDKP}=\frac{3}{4}S_{\triangle CSD}=\frac{195}{4}.
Пусть AQ
— высота четырёхугольной пирамиды ACDKP
с основанием CDKP
. Поскольку H
— середина наклонной AC
к плоскости CSD
, то расстояние AQ
вдвое больше расстояния от точки H
до плоскости CSD
(см. задачу 9180), т. е. высоты HN
прямоугольного треугольника SHM
, проведённой из вершины прямого угла. Значит (см. задачу 1967),
AQ=2HN=2\cdot\frac{HM\cdot SH}{SM}=2\cdot\frac{5\cdot12}{13}=\frac{120}{13}.
Следовательно,
V_{ACDKP}=\frac{1}{3}S_{CDKP}\cdot AQ=\frac{1}{3}\cdot\frac{195}{4}\cdot\frac{120}{13}=150.
Источник: ЕГЭ. — 2021, 7 июня, задача 14
