16072. Точка P
лежит внутри вписанного четырёхугольника ABCD
, причём \angle BPC=\angle BAP+\angle PDC
. Точки E
, F
и G
— проекции точки P
на AB
, AD
и DC
соответственно. Докажите, что треугольник FEG
подобен треугольнику PBC
.
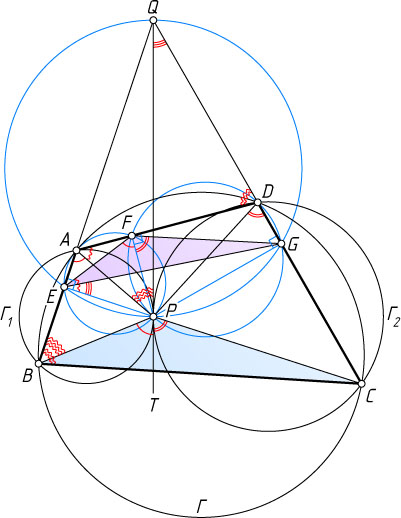
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть \Gamma
, \Gamma_{1}
и \Gamma_{2}
— описанные окружности четырёхугольника ABCD
и треугольников PAB
и PCD
соответственно.
От луча PB
в полуплоскость, содержащую точку C
, отложим угол BPT
, равный углу BAP
. Тогда
\angle TPC=\angle BPC-\angle BPT=\angle BPC-\angle BAP=\angle PDC.
Значит, прямая PT
касается и окружности \Gamma_{1}
, и окружности \Gamma_{2}
(см. задачу 144), а так как AB
и CD
— общие хорды окружностей \Gamma
, \Gamma_{1}
и \Gamma
, \Gamma_{2}
соответственно, то прямые PT
, AB
и CD
— радикальные оси окружностей \Gamma_{1}
и \Gamma_{2}
, \Gamma
и \Gamma_{1}
, \Gamma
и \Gamma_{2}
— пересекаются в радикальном центре Q
этих трёх окружностей (см. задачи 6392 и 6393).
Из точек E
и F
отрезок AP
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AP
. Тогда
\angle FEP=\angle FAP=\angle DAP.
Аналогично, точки F
, D
, G
и P
лежат на одной окружности, поэтому
\angle BPC=\angle BAP+\angle PDC=\angle EFP+\angle PFG=\angle EFG.
Из точек E
и G
отрезок PQ
виден под прямым углом, значит, эти точки лежат на окружности с диаметром PQ
, поэтому
\angle GEP=\angle GQP=\angle DQP.
Кроме того,
\angle DAP+\angle QPA=\angle QDA+\angle DQP.
Значит,
\angle FEG=\angle FEP-\angle GEP=\angle DAP-\angle DQP=\angle QDA-\angle QPA,
а так как четырёхугольник ABCD
вписанный, то \angle QDA=\angle QBC
. Кроме того, PQ
— касательная к окружности \Gamma_{1}
, поэтому \angle QPA=\angle PBA
. Таким образом,
\angle FEG=\angle QDA-\angle QPA=\angle QBC-\angle PBA=\angle PBC.
Следовательно, треугольник FEG
подобен треугольнику PBC
по двум углам. Что и требовалось доказать.
Если точка Q
лежит на продолжении стороны AB
за точку B
, решение аналогично, а если AB\parallel CD
, то PT\parallel AB\parallel CD
, то точки E
, P
и G
лежат на одной прямой, поэтому треугольники PAD
и PBC
равны (они симметричны относительно прямой EG
). Тогда из подобия треугольников FEG
и PAD
(по двум углам) следует подобие треугольников FEG
и PBC
.
Источник: Журнал «Crux Mathematicorum». — 1993, № 4, задача 1741 (1992, с. 138), с. 114
