2414. Теорема Паскаля для треугольника. Докажите, что касательные к описанной окружности треугольника, проведённые в его вершинах, пересекают прямые, содержащие противоположные стороны, в точках, лежащих на одной прямой.
Указание. Воспользуйтесь теоремой Менелая (см. задачу 1622) или её тригонометрической формой (см. задачу 1756).
Решение. Первый способ. Пусть касательные к описанной окружности треугольника ABC
, проходящие через точки A
, B
и C
, пересекаются с прямыми BC
, AC
и AB
в точках A_{1}
, B_{1}
и C_{1}
соответственно. Тогда
\frac{AB_{1}}{B_{1}C}=\left(\frac{AB}{BC}\right)^{2},~\frac{CA_{1}}{A_{1}B}=\left(\frac{AC}{AB}\right)^{2},~\frac{BC_{1}}{C_{1}A}=\left(\frac{BC}{AC}\right)^{2}
(см. задачу 196). Перемножив эти равенства, получим, что
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=\left(\frac{AB}{BC}\right)^{2}\cdot\left(\frac{AC}{AB}\right)^{2}\cdot\left(\frac{BC}{AC}\right)^{2}=1.
Следовательно, по теореме Менелая (см. задачу 1622) точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой.
Второй способ. Пусть касательная, проведённая в точке A
к окружности, описанной около неравнобедренного треугольника ABC
, пересекает прямую BC
в точке A_{1}
. Аналогично определим точки B_{1}
и C_{1}
. Обозначим \angle BAC=\alpha
, \angle ABC=\beta
, \angle ACB=\gamma
. Воспользуемся тригонометрической формой теоремы Менелая.
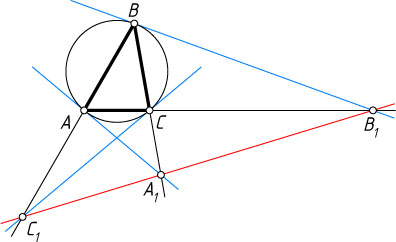
Рассмотрим случай, изображённый на рисунке. По теореме об угле между касательной и хордой
\angle ABB_{1}=\alpha+\beta,~\angle CBB_{1}=\alpha,~\angle BCC_{1}=\gamma+\beta=180^{\circ}-\alpha,
\angle ACC_{1}=\beta,~\angle CAA_{1}=\beta,~\angle BAA_{1}=\alpha+\beta.
Тогда
\frac{\sin\angle ABB_{1}}{\sin\angle CBB_{1}}\cdot\frac{\sin\angle BCC_{1}}{\sin\angle ACC_{1}}\cdot\frac{\sin\angle CAA_{1}}{\sin\angle BAA_{1}}=\frac{\sin(\alpha+\beta)}{\sin\alpha}\cdot\frac{\sin\alpha}{\sin\beta}\cdot\frac{\sin\beta}{\sin(\alpha+\beta)}=1
Следовательно, по теореме Менелая в тригонометрической форме (см. задачу 1756) точки A_{1}
, B_{1}
и C_{1}
лежат на одной прямой.
Аналогично для любого другого случая.
Примечание. Разбора случаев можно избежать, рассматривая ориентированные углы.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 347б, с. 42
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 76
