2416. Теорема Шлёмильха. Рассмотрим три прямые, каждая из которых проходит через середину высоты и середину стороны, на которую эта высота опущена. Докажите, что эти прямые пересекаются в одной точке.
Указание. К треугольнику с вершинами в серединах сторон данного примените утверждение задачи 2415 или примените теорему Чевы к треугольнику с вершинами в серединах сторон данного.
Решение. Первый способ. Пусть A_{2}
, B_{2}
и C_{2}
— середины высот соответственно AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
, A_{2}
, B_{2}
и C_{2}
— точки, соответственно симметричные точкам A_{1}
, B_{1}
и C_{1}
относительно середин K
, L
и M
сторон BC
, AC
и AB
соответственно.
Пусть серединный перпендикуляр к стороне BC
пересекается с прямой ML
в точке A_{3}
. Средняя линия ML
треугольника ABC
проходит через середину A_{2}
высоты AA_{1}
, а так как прямоугольные треугольники AA_{2}M
и KA_{3}L
равны по гипотенузе и острому углу, то A_{2}M=A_{3}L
. Значит, точки A_{2}
и A_{3}
симметричны относительно середины стороны ML
треугольника KLM
. Аналогично определим точки B_{3}
и C_{3}
и докажем, что они симметричны точкам B_{2}
и C_{2}
относительно середин сторон соответственно MK
и KL
треугольника KLM
.
Поскольку прямые KA_{3}
, LB_{3}
и MC_{3}
— серединные перпендикуляры к сторонам треугольника ABC
, они пересекаются в одной точке — центре описанной окружности треугольника ABC
. Следовательно, прямые A_{2}K
, B_{2}L
и C_{2}M
также пересекаются в одной точке (см. задачу 2415).
Второй способ. Пусть A_{2}
, B_{2}
и C_{2}
— середины высот соответственно AA_{1}
, BB_{1}
и CC_{1}
треугольника ABC
, K
, L
и M
— середины сторон BC
, AC
и AB
соответственно.
Точки A_{2}
, B_{2}
и C_{2}
лежат на средних линиях ML
, MK
и KL
треугольника ABC
, причём
\frac{MA_{2}}{A_{2}L}=\frac{BA_{1}}{A_{1}C},~\frac{LC_{2}}{C_{2}K}=\frac{AC_{1}}{C_{1}B},~\frac{KB_{2}}{B_{2}M}=\frac{CB_{1}}{B_{1}A}
(см. задачу 1597). Высоты треугольника пересекаются в одной точке, поэтому по теореме Чевы (см. задачу 1621)
\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Значит,
\frac{MA_{2}}{A_{2}L}\cdot\frac{LC_{2}}{C_{2}K}\cdot\frac{KB_{2}}{B_{2}M}=\frac{BA_{1}}{A_{1}C}\cdot\frac{CB_{1}}{B_{1}A}\cdot\frac{AC_{1}}{C_{1}B}=1.
Точки A_{2}
, B_{2}
, C_{2}
лежат на сторонах соответственно ML
, KM
и KL
треугольника KLM
, и при этом \frac{MA_{2}}{A_{2}L}\cdot\frac{LC_{2}}{C_{2}K}\cdot\frac{KB_{2}}{B_{2}M}=1
. Следовательно, по теореме Чевы прямые KA_{2}
, LB_{2}
и MC_{2}
пересекаются в одной точке.
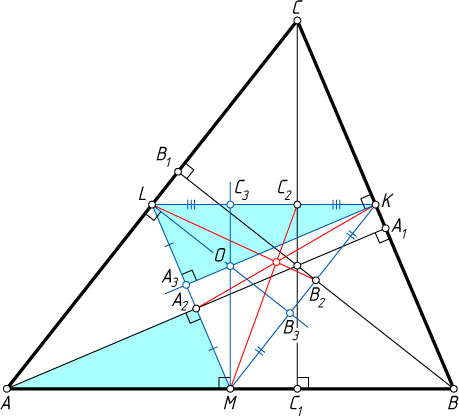
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — с. 133
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 151, с. 194
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 29
