2666. Найдите радиус окружности, описанной около треугольника со сторонами a
, b
и b
.
Ответ. \frac{b^{2}}{\sqrt{4b^{2}-a^{2}}}
.
Указание. Найдите синус угла при основании треугольника и воспользуйтесь теоремой синусов.
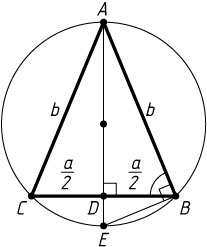
Решение. Первый способ. Пусть D
— середина основания BC
равнобедренного треугольника ABC
со сторонами AB=AC=b
и BC=a
. Из прямоугольного треугольника ADB
находим, что
\cos\angle ABD=\frac{BD}{AB}=\frac{a}{2b}.
Тогда
\sin\angle ABC=\sin\angle ABD=\sqrt{1-\cos^{2}\angle ABD}=\sqrt{1-\frac{a^{2}}{4b^{2}}}.
Следовательно, если R
— радиус окружности, описанной около треугольника ABC
, то
R=\frac{AC}{2\sin\angle ABC}=\frac{b}{2\sqrt{1-\frac{a^{2}}{4b^{2}}}}=\frac{b^{2}}{\sqrt{4b^{2}-a^{2}}}
(см. задачу 23).
Второй способ. Пусть O
— центр окружности радиуса R
, описанной около равнобедренного треугольника ABC
со сторонами AB=AC=b
и BC=a
, D
— середина основания BC
, E
— проекция точки O
на боковую сторону AC
. Тогда OA=R
, а E
— середина AC
.
Из прямоугольного треугольника ADC
находим, что
AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{b^{2}-\frac{a^{2}}{4}}.
Прямоугольные треугольники AOE
и ACD
подобны, поэтому \frac{AE}{OA}=\frac{AD}{AC}
, откуда
R=OA=\frac{AE\cdot AC}{AD}=\frac{\frac{b}{2}\cdot b}{\sqrt{b^{2}-\frac{a^{2}}{4}}}=\frac{b^{2}}{\sqrt{4b^{2}-a^{2}}}.
Третий способ. Пусть O
— центр окружности радиуса R
, описанной около равнобедренного треугольника ABC
со сторонами AB=AC=b
и BC=a
, D
— середина основания BC
, E
— проекция точки O
на боковую сторону AC
. Тогда OA=R
, а E
— середина AC
.
Из прямоугольного треугольника ADC
находим, что
AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{b^{2}-\frac{a^{2}}{4}}.
Продолжим отрезок AD
до пересечения с окружностью в точке A_{1}
. Тогда \angle ABA_{1}=90^{\circ}
(см. задачу 1689), а BD
— высота прямоугольного треугольника ABA_{1}
, проведённая из вершины прямого угла, поэтому (см. задачу 2728)
BD^{2}=AD\cdot DA_{1},~\mbox{или}~\frac{a^{2}}{4}=\left(2R-\sqrt{b^{2}-\frac{a^{2}}{4}}\right)\sqrt{b^{2}-\frac{a^{2}}{4}},
откуда находим, что
R=\frac{b^{2}}{\sqrt{4b^{2}-a^{2}}}.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 79
