2844. Теорема о радикальном центре трёх окружностей. На плоскости даны три попарно пересекающиеся окружности, центры которых не лежат на одной прямой. Докажите, что прямые, содержащие три общие хорды каждой пары этих окружностей, пересекаются в одной точке.
Указание. Используя теорему о произведениях отрезков пересекающихся хорд окружности или теорему о произведении всей секущей на её внешнюю часть, докажите, что одна из указанных прямых проходит через точку пересечения двух других.
Решение. Первый способ. Пусть окружности S_{1}
и S_{2}
пересекаются в точках A
и B
, окружности S_{1}
и S_{3}
— в точках C
и D
, окружности S_{2}
и S_{3}
— в точках E
и F
. Рассмотрим случай, когда попарно пересекаются отрезки AB
, CD
и EF
.
Если M
— точка пересечения отрезков CD
и EF
, то по теореме о произведениях отрезков пересекающихся хорд
CM\cdot MD=EM\cdot MF.
Через точки A
и M
проведём прямую, вторично пересекающую окружность S_{2}
в точке B_{1}
. Тогда хорды AB_{1}
и EF
окружности S_{2}
пересекаются в точке M
, поэтому
AM\cdot MB_{1}=EM\cdot MF=CM\cdot MD.
Значит точки A
, B_{1}
, C
и D
лежат на одной окружности (см. задачу 114), а так как через точки A
, C
и D
проходит единственная окружность S_{1}
, то точка B_{1}
лежит на окружности S_{1}
. Таким образом, точка B_{1}
является общей точкой окружностей S_{1}
и S_{2}
, отличной от точки A
. Значит, точка B_{1}
совпадает с точкой B
. Следовательно, хорда AB
проходит через точку пересечения хорд CD
и EF
.
Аналогично для случая когда пересекаются продолжения отрезков AB
, CD
и EF
.
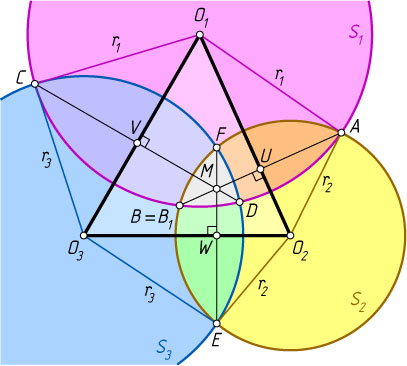
Второй способ. Пусть O_{1}
, O_{2}
и O_{3}
— центры окружностей S_{1}
, S_{2}
и S_{3}
радиусов r_{1}
, r_{2}
и r_{3}
соответственно, причём окружности S_{1}
и S_{2}
пересекаются в точках A
и B
, окружности S_{1}
и S_{3}
— в точках C
и D
, окружности S_{2}
и S_{3}
— в точках E
и F
.
Общая хорда двух пересекающихся окружностей перпендикулярна их линии центров, поэтому AB\perp O_{1}O_{2}
, CD\perp O_{1}O_{3}
и EF\perp O_{2}O_{3}
. Пусть U
, V
, W
— середины отрезков AB
, CD
, EF
соответственно. Тогда
O_{1}U^{2}-O_{2}U^{2}+O_{2}W^{2}-O_{3}W^{2}+O_{3}V^{2}-O_{1}V^{2}=
=O_{1}A^{2}-O_{2}A^{2}+O_{2}E^{2}-O_{3}E^{2}+O_{3}C^{2}-O_{1}C^{2}=
=r_{1}^{2}-r_{2}^{2}+r_{2}^{2}-r_{3}^{2}+r_{3}^{2}-r_{1}^{2}=0.
Применив теорему Карно к треугольнику O_{1}O_{2}O_{3}
и прямым AB
, CD
и EF
(см. задачу 2276), получим, что эти прямые пересекаются в одной точке. Что и требовалось доказать.
Третий способ. См. задачи 6392 и 6393.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 224, с. 230
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 116, с. 37
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 178, с. 19; № 275, с. 26
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 18, с. 38
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.56, с. 66
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.61, с. 63
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 315, с. 37
