3182. Высоты остроугольного неравнобедренного треугольника ABC
пересекаются в точке H
. Точки M
и N
— середины отрезков BC
и AH
соответственно. Докажите, что расстояние между точками пересечения прямой MN
с биссектрисами внешнего и внутреннего углов при вершине A
равно AH
.
Указание. Пусть O
— центр описанной окружности треугольника ABC
. Тогда AH=2OM
(см. задачу 1257) и \angle BAH=\angle CAO
(см. задачу 20).
Решение. Пусть биссектриса внутреннего угла при вершине A
треугольника ABC
пересекает сторону BC
в точке L
, O
— центр описанной окружности треугольника, прямая MN
пересекает биссектрису внутреннего угла при вершине A
в точке Q
, а биссектрису внешнего угла при этой вершине — в точке P
.
Воспользуемся следующими известными фактами: AH=2OM
(см. задачу 1257) и \angle BAH=\angle CAO
(см. задачу 20).
Поскольку AN=\frac{1}{2}AH=OM
и AN\parallel OM
, четырёхугольник ANMO
— параллелограмм. Поэтому MN\parallel OA
.
Поскольку AQ
— биссектриса угла BAC
и \angle BAH=\angle CAO
, луч AQ
— биссектриса угла NAO
. Поэтому \angle NQA=\angle OAQ=\angle NAQ
. Значит, треугольник ANQ
равнобедренный, NA=NQ
. Точка N
лежит на серединном перпендикуляре к отрезку AQ
, а так как треугольник APQ
прямоугольный (биссектрисы смежных углов перпендикулярны), то серединный перпендикуляр к его катету AQ
проходит через середину гипотенузы PQ
. Значит, AN
— медиана этого треугольника, проведённая из вершины прямого угла. Следовательно, PQ=2AN=AH
(см. задачу 1109). Что и требовалось доказать.
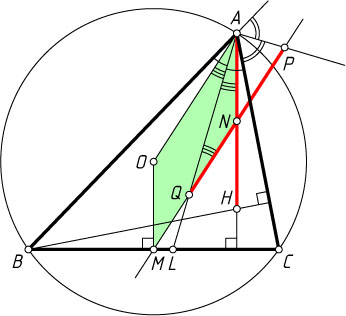
Источник: Журнал «Квант». — 2012, № 5-6, с. 59
