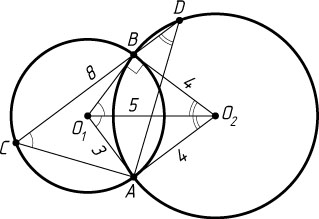
4808. Две окружности радиусов 3 и 4, расстояние между центрами которых равно 5, пересекаются в точках A
и B
. Через точку B
проведена прямая, пересекающая окружности в точках C
и D
, причём CD=8
и точка B
лежит между точками C
и D
. Найдите площадь треугольника ACD
.
Ответ. \frac{384}{25}
.
Решение. Пусть O_{1}
и O_{2}
— центры данных окружностей радиусов 3 и 4 соответственно. Треугольник O_{1}AO_{2}
прямоугольный с прямым углом при вершине A
, так как
AO_{1}^{2}+AO_{2}^{2}=9+16=25=O_{1}O_{2}^{2}
(см. задачу 1972).
Прямая O_{2}A
проходит через точку A
, лежащую на первой окружности, и перпендикулярна радиусу O_{1}A
этой окружности. Значит, прямая O_{2}A
— касательная к меньшей окружности (см. задачу 1735). Аналогично, прямая O_{1}A
— касательная к большей окружности.
Линия центров пересекающихся окружностей перпендикулярна их общей хорде и проходит через её середину H
(см. задачу 1130), поэтому \angle AO_{1}O_{2}=\frac{1}{2}\angle AO_{1}B
.
Пусть точка C
лежит на меньшей окружности. По теореме об угле между касательной и хордой
\angle ACD=\angle ACB=\frac{1}{2}\angle AO_{1}B=\angle AO_{1}O_{2}.
Аналогично, \angle ADC=\angle AO_{2}O_{1}
, значит, треугольники ACD
и AO_{1}O_{2}
подобны по двум углам, причём коэффициент подобия равен \frac{CD}{O_{1}O_{2}}=\frac{8}{5}
. Следовательно,
S_{\triangle ACD}=\left(\frac{8}{5}\right)^{2}S_{\triangle O_{1}AO_{2}}=\frac{64}{25}\cdot\frac{1}{2}\cdot3\cdot4=\frac{384}{25}.
Источник: Вступительный экзамен на физический факультет НГУ. — 1987, задача 3
Источник: Журнал «Квант». — 1988, № 3, с. 54, задача 3, вариант 2