6146. Высоты AD
и CE
треугольника ABC
пересекается в точке O
. Прямые AC
и DE
пересекаются в точке K
. Докажите, что прямая KO
перпендикулярна медиане BM
треугольника ABC
.
Решение. Первый способ. Заметим, что B
— точка пересечения высот треугольника AOC
, поэтому отрезок BO
вдвое больше расстояния от центра Q
описанной окружности треугольника AOC
до стороны AC
(см. задачу 1257).
Пусть F
— середина BO
. Тогда BF=QM
и BF\parallel QM
, значит, BFQM
— параллелограмм, поэтому BM\parallel FQ
.
Из точек D
и E
отрезок BO
виден под прямым углом, значит, точки D
, E
, B
и O
лежат на окружности \Omega
с диаметром BO
.
Пусть прямая KO
вторично пересекает эту окружность в точке P
. Тогда KO\cdot KP=KE\cdot KD=KA\cdot KC
, так как точки D
, E
, A
и C
также лежат на одной окружности. Значит, точка P
лежит на описанной окружности треугольника AOC
(см. задачу 114).
Таким образом, отрезок OP
— общая хорда окружности \Omega
с центром F
и описанной окружности треугольника AOC
, а так как общая хорда пересекающихся окружностей перпендикулярна их линии центров, то OP\perp QF
. Следовательно, KO\perp BM
. Что и требовалось доказать.
Второй способ. Из точек D
и E
отрезок BO
виден под прямым углом, значит, точки D
, E
, B
и O
лежат на окружности с диаметром BO
. Пусть L
— точка пересечения этой окружности с описанной окружностью треугольника ABC
. Тогда точки M
, O
и L
лежат на одной прямой (см. задачу 3180), а так как \angle BLO=90^{\circ}
, то ML\perp BL
.
Точки B
, K
и L
также лежат на одной прямой (см. задачу 10875), а ML\perp BL
, поэтому ML
— высота треугольника BKM
. Поскольку BO\perp KM
, точка O
— ортоцентр треугольника BKM
. Значит, отрезок KO
лежит на третьей высоте этого треугольника. Следовательно, KO\perp BM
.
Третий способ (М.Волчкевич). Докажем, что прямая OM
перпендикулярна KB
. Отсюда непосредственно будет следовать утверждение задачи, поскольку в этом случае точка O
окажется ортоцентром треугольника KBM
.
Пусть N
— основание перпендикуляра, опущенного из точки O
на прямую BK
. Поскольку точки E
, N
и D
лежат на окружности с диаметром OB
, то угол BND
равен углу BED
. Четырёхугольник AEDC
вписан в окружность с диаметром AC
, поэтому угол BED
равен углу ACB
. Таким образом, сумма углов KND
и ACB
равна 180^{\circ}
, т. е. четырёхугольник KNDC
вписанный. Значит, угол NCK
равен углу NDK
.
Точки B
, D
, E
и N
лежат на одной окружности, поэтому угол NDE
равен углу NBE
. Значит, равны углы NBA
и NCA
, т. е. точки A
, B
, C
и N
лежат на одной окружности — на описанной окружности треугольника ABC
.
Продолжим NO
до пересечения с описанной окружностью треугольника ABC
в точке G
. Угол BNP
прямой, поэтому BG
— диаметр этой окружности. Значит, углы BAG
и BCG
прямые. Значит, отрезок AG
параллелен CE
, а GC
параллелен AD
. Тогда AGCO
— параллелограмм, и прямая NO
делит AC
пополам. Что и требовалось доказать.
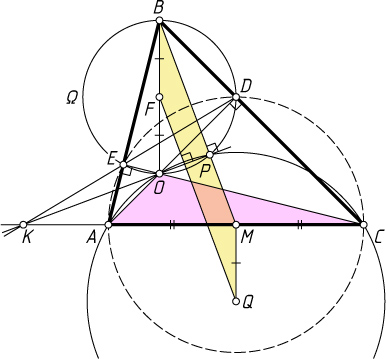
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Волчкевич М. А.
Автор: Ильясов С.
Источник: Журнал «Квант». — 2000, № 2, с. 12, М1724; 2010, № 4, с. 19, М2187; 2014, № 1, с. 44
Источник: Задачник «Кванта». — М1724
Источник: Журнал «Crux Mathematicorum». — 2005, № 3, задача 2, с. 163
Источник: Тайваньские математические олимпиады. — 2000
