6426. На сторонах AB
, BC
и CA
треугольника ABC
построены во внешнюю сторону квадраты ABB_{1}A_{2}
, BCC_{1}B_{2}
и CAA_{1}C_{2}
. Докажите, что перпендикуляры к отрезкам A_{1}A_{2}
, B_{1}B_{2}
и C_{1}C_{2}
, восставленные в их серединах, пересекаются в одной точке.
Указание. Докажите, что указанные перпендикуляры параллельны медианам треугольника ABC
.
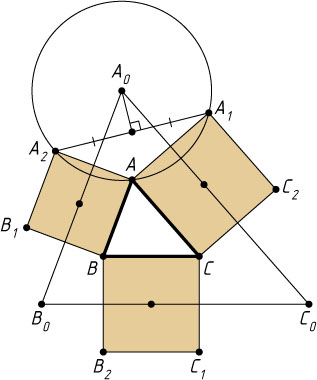
Решение. Через центр каждого квадрата проведём прямую, параллельную стороне треугольника, на которой построен этот квадрат. Пусть эти прямые пересекаются в точках A_{0}
, B_{0}
, C_{0}
. Тогда, например, A_{0}
— центр описанной окружности треугольника AA_{1}A_{2}
. Поэтому перпендикуляр, опущенный из точки A_{0}
на A_{1}A_{2}
, проходит через середину отрезка A_{1}A_{2}
. Аналогично для остальных вершин треугольника A_{0}B_{0}C_{0}
.
Медиана AA_{3}
треугольника ABC
перпендикулярна A_{1}A_{2}
(см. задачу 6006), поэтому серединный перпендикуляр к отрезку A_{1}A_{2}
параллелен этой медиане. Аналогично, медианы BB_{3}
и CC_{3}
треугольника ABC
параллельны серединным перпендикулярам к отрезкам B_{1}B_{2}
и C_{1}C_{2}
.
Треугольник A_{0}B_{0}C_{0}
гомотетичен треугольнику ABC
(см. задачу 5000). При этой гомотетии серединные перпендикуляры к отрезкам A_{1}A_{2}
, B_{1}B_{2}
, C_{1}C_{2}
переходят в параллельные им прямые, содержащие медианы треугольника ABC
, а так как медианы треугольника пересекаются в одной точке, то указанные серединные перпендикуляры также пересекаются в одной точке.
Примечание. Утверждение задачи остаётся верным, если заменить квадраты на произвольные прямоугольники со сторонами AB
, BC
и AC
(см. задачу 817).
Автор: Азамов Н. А.
Источник: Журнал «Квант». — 1986, № 4, с. 28, М982
Источник: Задачник «Кванта». — М982
