6453. Дан треугольник ABC
. В нём H
— точка пересечения высот, I
— центр вписанной окружности, O
— центр описанной окружности, K
— точка касания вписанной окружности со стороной BC
. Известно, что отрезки IO
и BC
параллельны. Докажите, что отрезки AO
и HK
также параллельны.
Решение. Известно, что в любом треугольнике расстояние от вершины до точки пересечения высот вдвое больше расстояния от центра описанной окружности до противоположной стороны (см. задачу 1257). Поэтому, если A_{1}
— середина стороны BC
, то AH=2OA_{1}
.
Поскольку OA_{1}KI
— прямоугольник, то OA_{1}=IK
. Поэтому AH=2OA_{1}=2IK
, т. е. отрезок AH
равен диаметру вписанной в треугольник ABC
окружности. Пусть M
— точка этой окружности, диаметрально противоположная точке K
. Поскольку AH\parallel KM
и AH=KM
, то AHKM
— параллелограмм, значит, AM\parallel HK
.
Рассмотрим гомотетию с центром в точке A
, переводящую вписанную окружность треугольника ABC
во вневписанную окружность этого треугольника, касающуюся стороны BC
. При этой гомотетии касательная к вписанной окружности, проведённая через точку M
, переходит в прямую BC
, значит, точка M
переходит в точку касания X
вневписанной окружности со стороной BC
.
Докажем, что BK=CX
. Пусть P
и Q
— точки касания рассматриваемой вневписанной окружности с продолжениями сторон AC
и BC
соответственно, p
— полупериметр треугольника ABC
. Тогда
CX=CP,~BX=BQ,
2p=AC+(CX+BX)+AB=(AC+CP)+(BQ+AB)=AP+AQ,
а так как AP=AQ
, то AP=AQ=p
. Тогда
CX=CP=AP-AC=p-AC=BK
(см. задачи 219 и 4805).
Из доказанного следует, что середина A_{1}
стороны BC
будет также серединой отрезка KX
.
Пусть прямые OA_{1}
и AX
пересекаются в точке O'
. Тогда A_{1}O'
— средняя линия треугольника KMX
, поэтому
O'A_{1}=\frac{1}{2}KM=\frac{1}{2}AH=OA_{1}.
Значит, точка O'
совпадает с точкой O
. Таким образом, точка O
лежит на прямой AM
, а так как AM\parallel HK
, то AO\parallel HK
, что и требовалось доказать.
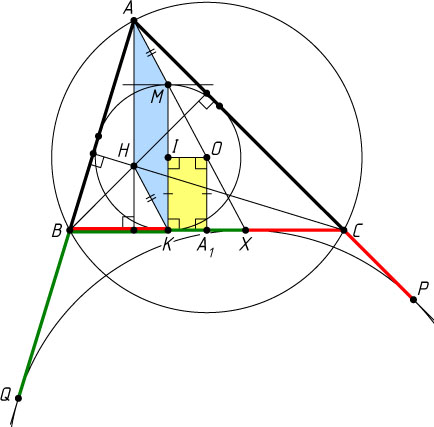
Автор: Кожевников П. А.
Источник: Турнир городов. — 2003-2004, XXV, осенний тур, старшие классы, основной вариант
