6635. Хорды AD
, BE
и CF
окружности делят друг друга на три равные части.
а) Докажите, что эти хорды равны.
б) Найдите площадь шестиугольника ABCDEF
, если точки A
, B
, C
, D
, E
и F
последовательно расположены на окружности, а радиус окружности равен 2\sqrt{21}
.
Ответ. 117\sqrt{3}
.
Решение. а) Пусть хорды AD
и BE
пересекаются в точке P
. Положим AD=3x
и BE=3y
. По теореме о произведении отрезков пересекающихся хорд AP\cdot PD=BP\cdot PE
(см. задачу 2627), или x\cdot2x=y\cdot2y
. Отсюда находим, что x=y
. Значит, AD=BE
. Аналогично AD=CF
.
б) Пусть хорды AD
и CF
пересекаются в точке Q
, а хорды BE
и CF
— в точке T
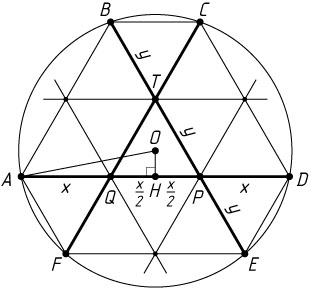
. Равные хорды равноудалены от центра окружности (см. задачу 1673), поэтому центр равностороннего треугольника PQT
совпадает с центром O
данной окружности.
Опустим перпендикуляр OH
из центра окружности на сторону PQ
. Тогда H
— середина AD
, а OH
— радиус вписанной окружности равностороннего треугольника PQT
со стороной x
. Значит (см. задачу 1963),
OH=\frac{x\sqrt{3}}{6},~AH=\frac{1}{2}AD=\frac{3x}{2}.
По теореме Пифагора OH^{2}+AH^{2}=OA^{2}
, или
\frac{1}{12}x^{2}+\frac{9}{4}x^{2}=(2\sqrt{21})^{2}.
Отсюда находим, что x=6
.
Через точки P
, Q
и T
проведём прямые, соответственно параллельные хордам CF
, BE
и AD
. Эти прямые и хорды CF
, BE
и AD
разбивают шестиугольник ABCDEF
на 13 равных равносторонних треугольников со стороной x
. Площадь каждого из них равна
\frac{1}{2}PQ\cdot TH=\frac{1}{2}x\cdot\frac{x\sqrt{3}}{2}=\frac{x^{2}\sqrt{3}}{4}.
Следовательно,
S_{ABCDEF}=13\cdot\frac{x^{2}\sqrt{3}}{4}=13\cdot\frac{36\sqrt{3}}{4}=13\cdot9\sqrt{3}=117\sqrt{3}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.43.1, с. 129
