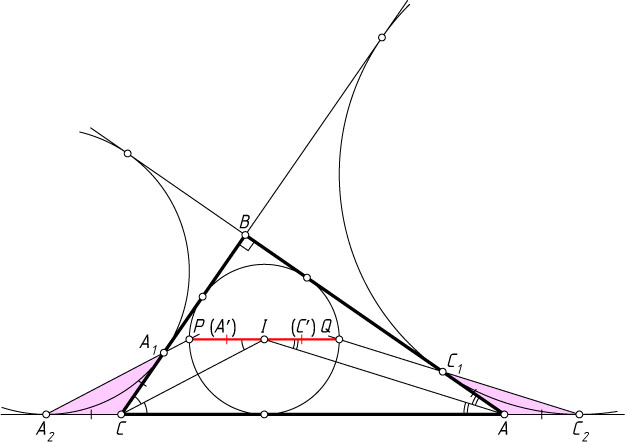
6645. Вневписанная окружность прямоугольного треугольника ABC
(\angle B=90^{\circ}
) касается стороны BC
в точке A_{1}
, а прямой AC
— в точке A_{2}
. Луч A_{2}A_{1}
пересекает первый раз окружность, вписанную в треугольник ABC
, в точке A'
. Аналогично определяется точка C'
. Докажите, что AC\parallel A'C'
.
Решение. Проведём через центр I
вписанной окружности радиуса r
диаметр PQ
, параллельный AC
. Заметим, что CI
— биссектриса внешнего угла при вершине C
равнобедренного треугольника A_{1}CA_{2}
, поэтому CI\parallel A_{1}A_{2}
(см. задачу 1174). Поскольку
\angle PIC=\angle ACI=\angle BCI,~CA_{1}=\frac{1}{2}(AB+BC-AC)=r=IP
(см. задачи 4805 и 217), прямые A_{1}P
и CI
параллельны (точки P
и A_{1}
равноудалены от прямой CI
). Поэтому прямая A_{1}P
совпадает с прямой A_{1}A_{2}
. Тогда точка P
совпадает с A'
. Аналогично точка Q
совпадает с C'
. Следовательно, AC\parallel A'C'
.
