6889. Через точку M
, расположенную внутри окружности, проведены три прямые, образующие друг с другом углы 60^{\circ}
и пересекающие окружность в точках A
, B
, C
, D
, E
и F
, последовательно расположенных на окружности. Докажите, что MA+MC+ME=MB+MD+MF
.
Указание. Проведите окружность, концентрическую данной и проходящую через точку M
. Далее см. задачу 17.
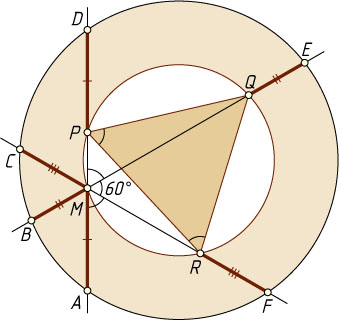
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть окружность, концентрическая данной и проходящая через точку M
, пересекает прямые AD
, BE
и CF
в точках P
, Q
и R
соответственно. Вписанные во вторую окружность углы PRQ
и PMQ
опираются на одну и ту же дугу, поэтому
\angle PRQ=\angle PMQ=\angle DME=60^{\circ}.
Аналогично \angle QPR=60^{\circ}
. Значит, треугольник PQR
равносторонний. Точка M
лежит на меньшей дуге PR
его описанной окружности, поэтому MQ=MP+MR
(см. задачу 17). Кроме того,
MA=PD,~MB=QE,~MC=RF
(см. задачу 483). Следовательно,
MA+MC+ME=PD+RF+BQ=
=(MD-MP)+(MF-MR)+(MB+MQ)=
=(MD+MF+MB)+(MQ-MP-MR)=MB+MD+MF.
Аналогично для всех остальных случаев.
Примечание. Используя результат задачи 4786, можно доказать более общее утверждение. Если через точку M
, расположенную внутри окружности, проведены n
хорд A_{1}B_{1}
, A_{2}B_{2}
, …, A_{n}B_{n}
под равными углами, причём n
не является степенью двойки, то
MA_{1}+MA_{2}+\dots+MA_{n}=MB_{1}+MB_{2}+\dots+MB_{n}.
Источник: Журнал «Crux Mathematicorum». — 1992, № 8, задача 7, с. 234
