6923. В трапеции ABCD
биссектрисы углов A
и D
пересекаются в точке E
, лежащей на боковой стороне BC
. Эти биссектрисы разбивают трапецию на три треугольника, в которые вписали окружности. Одна из этих окружностей касается основания AB
в точке K
, а две другие касаются биссектрисы DE
в точках M
и N
. Докажите, что BK=MN
.
Указание. См. задачи 1146, 219.
Решение. Заметим, что \angle AED=90^{\circ}
(см. задачу 1146) Докажем, что AD=AB+CD
и CE=BE
.
Пусть F
— точка пересечения прямых DE
и AB
. Тогда в треугольнике ADF
отрезок AE
является высотой и биссектрисой, следовательно, этот треугольник равнобедренный и DE=EF
. Треугольники DCE
и FBE
равны по стороне и двум прилежащим к ней углам. Следовательно, CE=BE
и DC=FB
, откуда
AD=AF=AB+BF=AB+CD.
В дальнейших рассуждениях несколько раз воспользуемся следующим фактом: если p
— полупериметр треугольника ABC
, а A_{1}
, B_{1}
и C_{1}
— точки касания вписанной окружности со сторонами BC
, AC
и AB
соответственно, то AB_{1}=p-BC
(см. задачу 219).
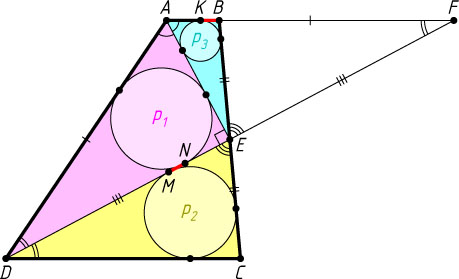
Пусть вписанная окружность треугольника ABE
касается стороны AB
в точке K
, вписанные окружности треугольников CDE
и ADE
касаются общей стороны DE
в точках M
и N
соответственно, а полупериметры треугольников ADE
, DCE
и ABE
равны p_{1}
, p_{2}
и p_{3}
соответственно. Тогда
MN=DN-DM=p_{1}-AE-(p_{2}-CE),~BK=p_{3}-AE.
Значит,
MN-BK=p_{1}-p_{2}-p_{3}+CE=\frac{1}{2}(AD+DE+AE-
-DC-CE-DE-AB-AE-BE+2CE)=0,
что и требовалось. (Точки M
и N
расположены на отрезке DE
именно в таком порядке, как показано на рисунке, в силу равенства (DN-DM)-BK=0
, т. е. DN\gt DM
.)
Примечание. Отметим, что поскольку AD=AB+DC
, а DE
и AE
— биссектрисы углов D
и A
соответственно, то треугольники DCE
и ABE
можно «перегнуть» по сторонам DE
и AE
внутрь треугольника ADE
так, что точки C
и B
совпадут и окажутся на отрезке AD
. Следовательно, данную задачу можно было свести к задаче 5418.
Подробнее, например, см. статью А.Блинкова и Ю.Блинкова «Две окружности в треугольнике, три окружности в треугольнике...», Квант, 2012, N2, с.45-49.
Автор: Штейнгарц Л. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2015, 8-9 класс
Источник: Московская устная олимпиада по геометрии. — 2015, № 4, 8-9 классы
