6938. В равнобедренную трапецию, периметр которой равен 220, а площадь равна 2420, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Ответ. 8,8.
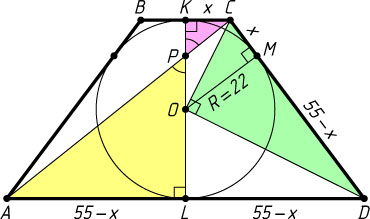
Решение. Пусть BC\lt AD
— основания данной трапеции ABCD
, O
— центр её вписанной окружности радиуса R
, окружность касается сторон BC
, AD
и CD
в точках K
, L
и M
соответственно, P
— точка пересечения диагоналей. Трапеция равнобедренная, поэтому точки K
, P
, O
и L
лежат на одной прямой — на диаметре окружности, а K
и L
— середины оснований.
Радиус окружности, вписанной в четырёхугольник равен площади четырёхугольника, делённой на его полупериметр (см. задачу 523), значит, R=\frac{2420}{110}=22
. Суммы противоположных сторон описанного четырёхугольника равны (см. задачу 310), поэтому
2CD=AB+CD=BC+AD=\frac{1}{2}\cdot220=110,~CD=55.
Обозначим, CK=CM=x
. Тогда DL=DM=55-x
. Треугольник COD
прямоугольный с прямым углом при вершине O
(см. задачу 313), отрезок OM=R
— его высота, проведённая из вершины прямого угла, поэтому
CM=\frac{OM^{2}}{MD},~x=\frac{22^{2}}{55-x},~x^{2}-55x+484=0,
откуда находим, что x=11
или x=44
, а так как BC\lt AD
, то x\lt55-x
. Значит CK=CM=x=11
и AL=DL=DM=55-x=44
.
Прямоугольные треугольники CPK
и APL
подобны с коэффициентом \frac{CK}{AL}=\frac{11}{44}=\frac{1}{4}
, следовательно,
PK=\frac{1}{5}KL=\frac{1}{5}\cdot2R=\frac{1}{5}\cdot44=8{,}8.
Источник: Диагностические и тренировочные задачи ОГЭ (ГИА). — 2016, задача 26
