8300. Высота равногранного тетраэдра равна h
, а высота грани делится точкой пересечения высот этой грани на отрезки, равные h_{1}
и h_{2}
. Докажите, что h^{2}=4h_{1}h_{2}
.
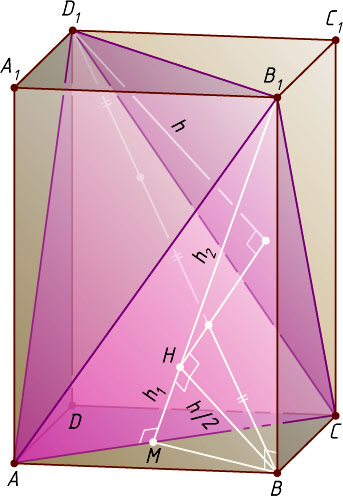
Решение. (Решение А.Буряка.) Пусть ACB_{1}D_{1}
— равногранный тетраэдр. Рассмотрим его описанный параллелепипед ABCDA_{1}B_{1}C_{1}D_{1}
. Этот параллелепипед прямоугольный, так как тетраэдр равногранный (см. задачу 7994).
Плоскость AB_{1}C
делит диагональ BD_{1}
в отношении 1:2
, считая от точки B
(см. задачу 7212), поэтому расстояние от точки D_{1}
до этой плоскости, т. е. высота тетраэдра ACB_{1}D_{1}
, вдвое больше расстояния до этой плоскости от точки B
. Пусть BH
— перпендикуляр, опущенный из точки B
на плоскость AB_{1}C
. Тогда BH=\frac{h}{2}
.
Рассмотрим тетраэдр ABCB_{1}
. Его противоположные рёбра попарно перпендикулярны, поэтому его высоты пересекаются в одной точке, т. е. этот тетраэдр ортоцентрический (см. задачу 7807). Каждая его высота, в частности BH
, проходит через ортоцентр грани (см. задачу 9293), поэтому H
— ортоцентр треугольника AB_{1}C
.
Пусть прямая B_{1}H
пересекает AC
в точке M
. Тогда MH=h_{1}
и B_{1}H=h_{2}
, а так как BH
— высота прямоугольного треугольника MBB_{1}
, проведённая из вершины прямого угла, то
\frac{h^{2}}{4}=BH^{2}=MH\cdot B_{1}H=h_{1}h_{2},
откуда h^{2}=4h_{1}h_{2}
. Что и требовалось доказать.
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 6.33б, с. 104
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 8.40б, с. 112
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 325, с. 44
