9597. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
все рёбра равны 2. Точка M
— середина ребра AA_{1}
.
а) Докажите, что прямые MB
и B_{1}C
перпендикулярны.
б) Найдите расстояние между прямыми MB
и B_{1}C
.
Ответ. \frac{\sqrt{30}}{5}
.
Решение. а)
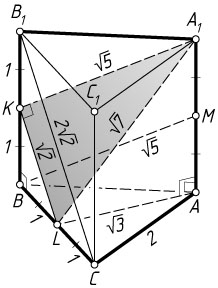
Первый способ. Пусть K
и L
— середины рёбер BB_{1}
и BC
соответственно. Тогда A_{1}MBK
— параллелограмм, поэтому A_{1}K\parallel MB
. Отрезок KL
— средняя линия треугольника BB_{1}C
, поэтому KL\parallel B_{1}C
. Значит, угол между скрещивающимися прямыми MB
и B_{1}C
равен углу между пересекающимися прямыми A_{1}K
и KL
.
Отрезок AL
— высота равностороннего треугольника со стороной 2, поэтому AL=\frac{2\sqrt{3}}{2}=\sqrt{3}
. Из прямоугольных треугольников AMB
, BB_{1}C
и AA_{1}L
находим, что
BM=\sqrt{AM^{2}+AB^{2}}=\sqrt{1+4}=\sqrt{5},~B_{1}C=BC\sqrt{2}=2\sqrt{2},
A_{1}L=\sqrt{AA_{1}^{2}+AL^{2}}=\sqrt{4+3}=\sqrt{7}.
Значит, в треугольнике A_{1}KL
известны стороны
A_{1}K=BM=\sqrt{5},~KL=\frac{1}{2}B_{1}C=\sqrt{2},~A_{1}L=\sqrt{7},
а так как A_{1}K^{2}+KL^{2}=5+2=7=A_{1}L^{2}
, то \angle A_{1}KL=90^{\circ}
, т. е. прямые A_{1}K
и KL
перпендикулярны. Следовательно, параллельные им прямые MB
и B_{1}C
также перпендикулярны.
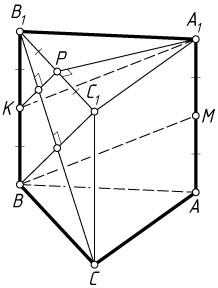
Второй способ. Пусть K
и P
— середины рёбер BB_{1}
и B_{1}C_{1}
соответственно. Тогда A_{1}P
— перпендикуляр к плоскости BCB_{1}
, а PK
— ортогональная проекция наклонной A_{1}K
на эту плоскость. Прямая B_{1}C
, лежащая в этой плоскости, перпендикулярна KP
, так как она перпендикулярна прямой BC_{1}
, параллельной KP
, значит, по теореме о трёх перпендикулярах прямая A_{1}K
перпендикулярна B_{1}C
. Следовательно, параллельная ей прямая MB
также перпендикулярна B_{1}C
.
б)
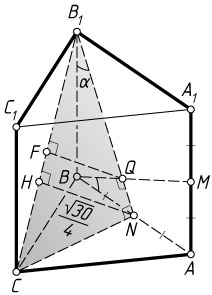
Первый способ. Пусть N
— середина ребра AB
, Q
— точка пересечения отрезков B_{1}N
и BM
. Обозначим \angle BB_{1}N=\angle ABM=\alpha
. Тогда \angle BNB_{1}=90^{\circ}-\alpha
, значит,
\angle BQN=180^{\circ}-\angle ABM-\angle BNB_{1}=180^{\circ}-\alpha-(90^{\circ}-\alpha)=90^{\circ},
т. е. BM\perp B_{1}N
.
Прямая BM
перпендикулярна двум пересекающимся прямым B_{1}N
и B_{1}C
плоскости B_{1}CN
, поэтому прямая BM
перпендикулярна плоскости B_{1}CN
, а значит, и любой прямой лежащей в этой плоскости, в частности, прямой QF
, где F
— основание перпендикуляра, опущенного из точки Q
на прямую B_{1}C
. Следовательно, QF
— общий перпендикуляр скрещивающихся прямых BM
и B_{1}C
.
Поскольку CN
— перпендикуляр к плоскости ABB_{1}
, треугольник CNB_{1}
прямоугольный. Пусть NH
— его высота. Тогда
NH=\frac{CN\cdot B_{1}N}{B_{1}C}=\frac{\sqrt{3}\cdot\sqrt{5}}{2\sqrt{2}}=\frac{\sqrt{30}}{4}
(см. задачу 1967).
Отрезок BQ
— высота прямоугольного треугольника NBB_{1}
, проведённая из вершины прямого угла, поэтому (см. задачу 2728)
\frac{B_{1}Q}{QN}=\frac{\frac{BB_{1}^{2}}{B_{1}N}}{\frac{BN^{2}}{B_{1}N}}=\frac{BB_{1}^{2}}{BN^{2}}=\frac{4}{1}=4.
Треугольник QFB_{1}
подобен треугольнику NHB_{1}
с коэффициентом \frac{B_{1}Q}{B_{1}N}=\frac{4}{5}
. Следовательно,
QF=\frac{4}{5}NH=\frac{4}{5}\cdot\frac{\sqrt{30}}{4}=\frac{\sqrt{30}}{5}.
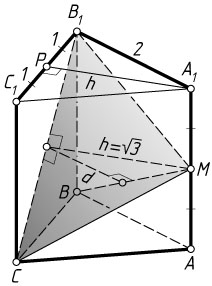
Второй способ. Пусть высота тетраэдра MBCB_{1}
, опущенная из его вершины M
на плоскость основания BB_{1}C
, равна h
. Точка M
лежит на прямой AA_{1}
, параллельной этой плоскости, поэтому расстояние от точки A_{1}
до плоскости BB_{1}C
также равно h
. С другой стороны, это расстояние равно высоте A_{1}P
равностороннего треугольника A_{1}B_{1}C_{1}
, т. е. h=\sqrt{3}
.
Пусть d
— искомое расстояние между скрещивающимися прямыми MB
и B_{1}C
, а V
— объём тетраэдра MBCB_{1}
. Тогда
V=\frac{1}{3}S_{\triangle BCB_{1}}\cdot h=\frac{1}{3}\cdot\frac{1}{2}AA_{1}\cdot AB\cdot h=\frac{1}{3}\cdot\frac{1}{2}\cdot2\cdot2\cdot\sqrt{3}=\frac{2\sqrt{3}}{3}.
С другой стороны
V=\frac{1}{6}MB\cdot B_{1}C\cdot d\sin90^{\circ}=\frac{1}{6}\cdot\sqrt{5}\cdot2\sqrt{2}\cdot d=\frac{d\sqrt{10}}{3}
(см. задачу 7234). Из равенства
\frac{d\sqrt{10}}{3}=\frac{2\sqrt{3}}{3}
находим, что d=\frac{\sqrt{30}}{5}
.
Источник: ЕГЭ. — 2018, досрочный экзамен, резервный день 11 апреля



