9598. На ребре AA_{1}
правильной четырёхугольной призмы ABCDA_{1}B_{1}C_{1}D_{1}
отмечена точка K
, причём AK:KA_{1}=1:3
. Через точки K
и B
проведена плоскость \alpha
, параллельная прямой AC
и пересекающая ребро DD_{1}
в точке M
.
а) Докажите, что точка M
— середина ребра DD_{1}
.
б) Найдите площадь сечения призмы плоскостью \alpha
, если AB=5
, AA_{1}=4
.
Ответ. 15\sqrt{3}
.
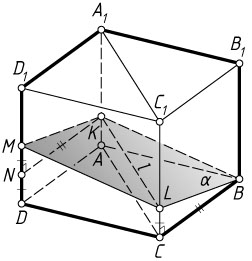
Решение. а) Плоскость AA_{1}C_{1}C
проходит через прямую AC
, параллельную плоскости \alpha
, и имеет с плоскостью \alpha
общую точку K
, значит, эти плоскости пересекаются по прямой l
, проходящей через точку K
параллельно AC
(см. задачу 8003). Пусть прямая l
пересекает ребро CC_{1}
в точке L
. Тогда плоскости \alpha
и BB_{1}C_{1}C
пересекаются по прямой BL
, причём CL:LC_{1}=AK:KA_{1}=1:3
.
Плоскость \alpha
пересекает параллельные плоскости AA_{1}D_{1}D
и BB_{1}C_{1}C
по параллельным прямым BL
и KM
(см. задачу 8009). Пусть прямая, проходящая через точку K
параллельно AD
, пересекает ребро DD_{1}
в точке N
. Тогда
DN=AK=\frac{1}{4}AA_{1}=\frac{1}{4}DD_{1}.
Из равенства треугольников KNM
и BCL
следует, что
MN=LC=\frac{1}{4}CC_{1}=\frac{1}{4}DD_{1}.
Значит,
DM=DN+MN=\frac{1}{4}DD_{1}+\frac{1}{4}DD_{1}=\frac{1}{2}DD_{1}.
Следовательно, точка M
— середина ребра DD_{1}
.
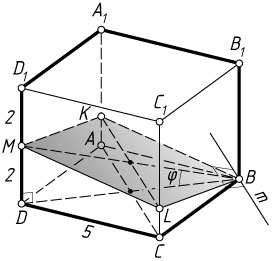
б) Плоскость \alpha
проходит через прямую KL
, параллельную плоскости ABCD
, и пересекает эту плоскость по прямой m
, проходящей через точку B
параллельно KL
, а значит, и AC
. По теореме о трёх перпендикулярах m\perp MB
, поэтому DBM
— линейный угол двугранного угла \varphi
, образованного плоскостями \alpha
и ABCD
. Из прямоугольного треугольника BDM
находим, что
\tg\varphi=\frac{DM}{BD}=\frac{2}{5\sqrt{2}}=\frac{\sqrt{2}}{5}.
Тогда
\cos\varphi=\frac{1}{\sqrt{1+\tg^{2}\varphi}}=\frac{1}{\sqrt{1+\frac{2}{25}}}=\frac{5}{\sqrt{27}}=\frac{5}{3\sqrt{3}}.
Ортогональная проекция сечения BLMK
на плоскость ABCD
— квадрат ABCD
, площадь которого равна 25. Следовательно, площадь сечения равна
\frac{25}{\cos\varphi}=\frac{25}{\frac{5}{3\sqrt{3}}}=15\sqrt{3}
(см. задачу 8093).
Источник: ЕГЭ. — 2018, досрочный экзамен, 30 марта

