9639. Дан куб с ребром a
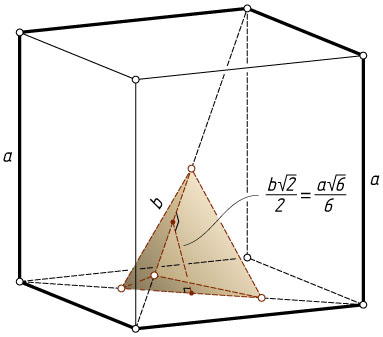
. Две вершины правильного тетраэдра лежат на его диагонали, а две оставшиеся вершины — на диагонали грани. Найдите объём тетраэдра.
Ответ. \frac{a^{3}\sqrt{6}}{108}
.
Решение. Расстояние между диагональю куба с ребром a
и скрещивающейся с ней диагональю грани куба равно \frac{a\sqrt{6}}{6}
(см. задачу 7174). Расстояние между противоположными рёбрами правильного тетраэдра с ребром b
равно \frac{b\sqrt{2}}{2}
(см. задачу 7046). Из равенства \frac{b\sqrt{2}}{2}=\frac{a\sqrt{6}}{6}
получаем, что b=\frac{a\sqrt{3}}{3}
.
Пусть V
— искомый объём правильного тетраэдра. Тогда (см. задачу 8461)
V=\frac{1}{3}\cdot\frac{b^{2}\sqrt{3}}{4}\cdot b\sqrt{\frac{2}{3}}=\frac{b^{3}\sqrt{2}}{12}=\frac{\left(\frac{a\sqrt{3}}{3}\right)^{3}\cdot\sqrt{2}}{12}=\frac{a^{3}\sqrt{6}}{108}.
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 18, с. 6
