9650. Ребро правильного тетраэдра равно a
. Плоскость P
проходит через вершину B
и середины рёбер AC
и AD
. Шар касается прямых AB
, AC
, AD
и той части плоскости P
, которая заключена внутри тетраэдра. Найдите радиус шара.
Ответ. \frac{a\sqrt{2}}{5\pm\sqrt{11}}
.
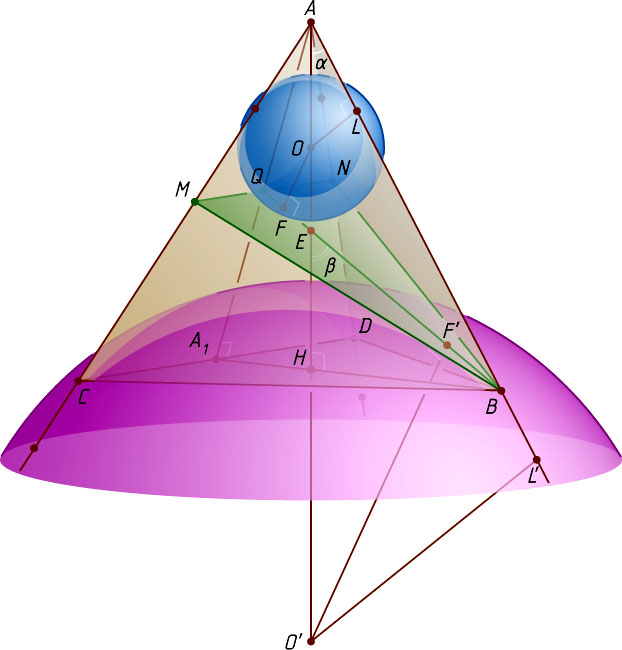
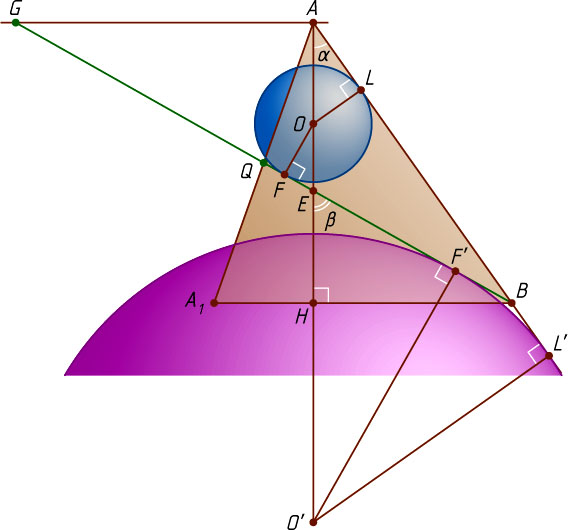
Решение. Пусть Q
— центр грани BCD
, E
и F
— середины рёбер AC
и AD
соответственно, N
— точка пересечения высоты AQ
тетраэдра с секущей плоскостью BEF
, K
— точка пересечения медианы AL
грани ACD
со средней линией EF
треугольника ACD
. Тогда AL=BL=\frac{a\sqrt{3}}{2}
, а так как BK
— медиана треугольника ABL
, то (см. задачу 4014)
BK=\frac{1}{2}\sqrt{2AD^{2}+2BL^{2}-AL^{2}}=\frac{1}{2}\sqrt{2AD^{2}+BL^{2}}=\frac{1}{2}\sqrt{2a^{2}+\frac{3}{4}a^{2}}=\frac{a\sqrt{11}}{4}.
Рассмотрим треугольник BKL
и прямую AQ
. По теореме Менелая (см. задачу 1622)
1=\frac{BN}{NK}\cdot\frac{KA}{AL}\cdot\frac{LQ}{QB}=\frac{BN}{NK}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{BN}{NK}\cdot\frac{1}{4},
откуда \frac{BN}{NK}=4
. Значит,
BN=\frac{4}{5}BK=\frac{a\sqrt{11}}{5}.
Искомый шар вписан в трёхгранный угол, все плоские углы которого равны, значит, центр шара лежит на прямой AQ
. Рассмотрим случай, когда центр O
шара и вершина A
лежат по одну сторону от секущей плоскости. Тогда искомый радиус r
равен радиусу окружности с центром на стороне AN
треугольника ABN
, касающейся стороны AB
и прямой BN
, следовательно (см. задачу 453),
r=\frac{2S_{\triangle ABN}}{AB+BN}=\frac{2\cdot\frac{4}{5}S_{\triangle ABK}}{AB+BN}=\frac{\frac{4}{5}S_{\triangle ABL}}{AB+BN}=
=\frac{\frac{4}{5}\cdot\frac{1}{2}DL\cdot AQ}{AB+BN}=\frac{\frac{2}{5}\cdot\frac{a\sqrt{3}}{2}\cdot a\sqrt{\frac{2}{3}}}{a+\frac{a\sqrt{11}}{5}}=\frac{a\sqrt{2}}{5+\sqrt{11}}.
Пусть теперь центр O_{1}
шара и вершина A
лежат по разные стороны от секущей плоскости. Тогда искомый радиус r
равен радиусу окружности с центром на луче AN
, касающейся стороны BN
и продолжения стороны AB
. В этом случае аналогично находим, что
r_{1}=\frac{2S_{\triangle ABN}}{AB-BN}=\frac{a\sqrt{2}}{5-\sqrt{11}}.
Докажем, что оба решения удовлетворяют условию задачи. Пусть H
и H_{1}
— точки касания первой сферы и второй сфер с секущей плоскостью. Тогда точка H
лежит на луче NK
. Обозначим \angle ONH=\angle QNB=\alpha
. Тогда
\sin\alpha=\frac{BQ}{BN}=\frac{\frac{a\sqrt{3}}{2}}{\frac{a\sqrt{11}}{5}}=\frac{5}{\sqrt{33}},~\ctg\alpha=\sqrt{\frac{1}{\sin^{2}\alpha}-1}=\frac{2\sqrt{2}}{5},
NH=OH\ctg\alpha=r\ctg\alpha=\frac{a\sqrt{2}}{5+\sqrt{11}}\cdot\frac{2\sqrt{2}}{5}=\frac{4a}{5(5+\sqrt{11})},
BH=BN+NH=\frac{a\sqrt{11}}{5}+\frac{4a}{5(5+\sqrt{11})}=\frac{a(3+\sqrt{11})}{5+\sqrt{11}}=
=\frac{a(3+\sqrt{11})(5-\sqrt{11})}{25-11}=\frac{a(\sqrt{11}+2)}{7}\lt\frac{a\sqrt{11}}{4}=BK
\left(\frac{\sqrt{11}+2}{7}\lt\frac{\sqrt{11}}{4}~\Leftrightarrow~4\sqrt{11}+8\lt7\sqrt{11}~\Leftrightarrow~8\lt3\sqrt{11}~\Leftrightarrow~64\lt99\right)
т. е. точка H
лежит внутри треугольника сечения.
То, что r_{1}
удовлетворяет условию задачи, очевидно (точки H
и H_{1}
лежат на прямой BK
по разные стороны от точки N
).
Источник: Вступительный экзамен в МФТИ. — 1972, билет 6, № 5
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 72-6-5, с. 154
Источник: Шарыгин И. Ф. Геометрия. Стереометрия: Задачник для 10—11 кл. — М.: Дрофа, 1998. — № 105, с. 16

