181. Дан треугольник ABC
. Окружность проходит через вершины A
, B
и пересекает стороны AC
и BC
в точках P
и Q
соответственно. На стороне AB
взяты точки R
и S
, причём QR\parallel CA
, PS\parallel CB
. Докажите, что точки P
, Q
, R
, S
лежат на одной окружности.
Указание. Дуги, заключённые между параллельными хордами, равны.
Решение. Продолжим QR
до пересечения с окружностью в точке Q_{1}
, а PS
— в точке P_{1}
. Пусть хорды PP_{1}
и QQ_{1}
пересекаются в точке T
.
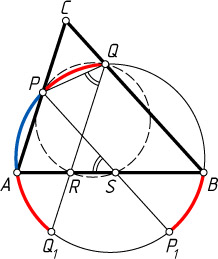
Рассмотрим случай, точки T
и C
лежат по одну сторону от прямой AB
(рис. 1). Тогда
\angle PQR=\angle PQQ_{1}=\frac{\cup PA+\cup AQ_{1}}{2},~\angle PSA=\frac{\cup PA+\cup BP_{1}}{2}
(см. задачи 26 и 1678). Поскольку
\cup BP_{1}=\cup PQ=\cup AQ_{1},
то \angle PQR=\angle PSR
. Следовательно, точки P
, Q
, R
и S
лежат на одной окружности (см. задачу 12).
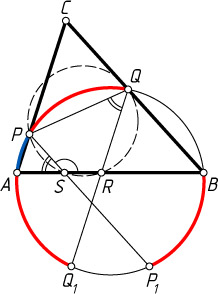
Пусть теперь точки T
и S
лежат по разные стороны от прямой AB
(рис. 2). Тогда
\angle ARP=\frac{\cup PA+\cup P_{1}B}{2}=\frac{\cup PA+\cup PQ}{2}=
=\frac{\cup PA+\cup AQ_{1}}{2}=\frac{\cup APQ}{2}=\angle PQQ_{1}=\angle PQS.
Значит,
\angle PRS=180^{\circ}-\angle ARP=180^{\circ}-\angle PQS,
поэтому четырёхугольник PQSR
вписанный (см. задачу 42). Следовательно, точки P
, Q
, R
и S
лежат на одной окружности
Примечание. Разбора случаев можно избежать, если рассматривать ориентированные углы.
Источник: Всероссийская олимпиада школьников. — 1988, XIV
Источник: Журнал «Квант». — 1988, № 10, с. 56, задача 2

