952. В треугольник ABC
вписана окружность. Касательная к этой окружности, параллельная стороне BC
, пересекает сторону AB
в точке D
и сторону AC
в точке E
. Периметры треугольников ABC
и ADE
равны соответственно 40 и 30, а угол ABC
равен \alpha
. Найдите радиус окружности.
Ответ. \frac{15\tg\frac{\alpha}{2}}{3+4\tg^{2}\frac{\alpha}{2}}=\frac{15\sin\alpha}{7-\cos\alpha}
.
Указание. Пусть M
— точка касания данной окружности со стороной AB
. Выразите отрезки BM
и DM
через радиус окружности и угол \alpha
и воспользуйтесь подобием треугольников ADE
и ABC
.
Решение. Первый способ. Треугольники ADE
и ABC
подобны с коэффициентом подобия, равным отношению их периметров, т. е. \frac{3}{4}
.
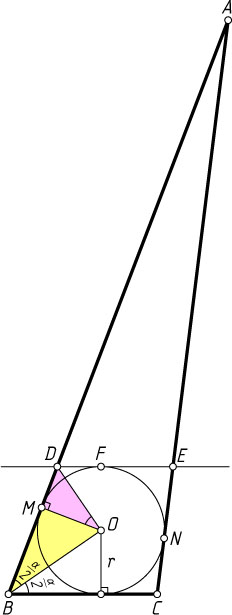
Пусть O
— центр данной окружности, r
— её радиус, M
— точка касания со стороной AB
. Из прямоугольных треугольников BMO
и OMD
(см. задачу 313) находим, что
BM=\frac{OM}{\tg\angle MBO}=\frac{r}{\tg\frac{\alpha}{2}},~MD=MO\tg\angle DOM=r\tg\frac{\alpha}{2}.
Поэтому
BD=BM+MD=r\left(\frac{1}{\tg\frac{\alpha}{2}}+\tg\frac{\alpha}{2}\right)=\frac{r\left(\tg^{2}\frac{\alpha}{2}+1\right)}{\tg\frac{\alpha}{2}}.
Пусть F
— точка касания данной окружности с отрезком DE
, а N
— со стороной AC
. Тогда
AM=AN,~AM+AN=AD+DE+AE=30.
Поэтому
AM=15,~AD=AM-MD=15-r\tg\frac{\alpha}{2}.
Поскольку \frac{AD}{AB}=\frac{3}{4}
, то
AD=3BD,~\mbox{или}~15-r\tg\frac{\alpha}{2}=\frac{3r\left(\tg^{2}\frac{\alpha}{2}+1\right)}{\tg\frac{\alpha}{2}}.
Откуда находим, что
r=\frac{15\tg\frac{\alpha}{2}}{3+4\tg^{2}\frac{\alpha}{2}}.
Второй способ. Пусть O
— центр данной окружности, r
— её радиус, M
— точка касания со стороной AB
, S
— площадь треугольника ABC
, p=20
— полупериметр треугольника ABC
, p_{1}=15
— полупериметр треугольника ADE
.
Тогда
AM=p-BC=20-BC~\mbox{и}~AM=p_{1}=15
(см. задачи 219 и 1750). Из равенства 20-BC=15
находим, что BC=5
.
Из прямоугольного треугольника BMO
находим, что BM=r\ctg\frac{\alpha}{2}
, значит,
AB=AM+BM=15+r\ctg\frac{\alpha}{2}.
Приравнивая правые части равенств S=pr
(см. задачу 452) и S=\frac{1}{2}AB\cdot BC\sin\alpha
, получим уравнение
20r=\frac{1}{2}(15+r\ctg\frac{\alpha}{2})\cdot5\sin\alpha,
из которого находим, что
r=\frac{15\sin\alpha}{8-\ctg\frac{\alpha}{2}\sin\alpha}=\frac{15\sin\alpha}{7-\cos\alpha}
(так как \ctg\frac{\alpha}{2}=\frac{1+\cos\alpha}{\sin\alpha}
).
Примечание. Из второго способа решения видно, что условие DE\parallel BC
лишнее.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1986, вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — , с. 172
