10709. Касательные к описанной окружности остроугольного треугольника ABC
в точках B
и C
пересекаются в точке A_{1}
, в точках A
и C
— в B_{1}
, в точках A
и B
— в C_{1}
. Прямые BC
и B_{1}C_{1}
пересекаются в точке A_{2}
, прямые AC
и A_{1}C_{1}
— в точке B_{2}
, прямые AB
и A_{1}B_{1}
— в точке C_{2}
; AH
— высота треугольника ABC
. Докажите, что:
а) треугольник A_{1}B_{1}C_{1}
подобен ортотреугольнику треугольника ABC
;
б) точки A_{2}
, B_{2}
и C_{2}
лежат на одной прямой;
в) HA
— биссектриса угла B_{1}HC_{1}
.
Указание. См. задачи 700, 1622, 178.
Решение. а) Стороны треугольника A_{1}B_{1}C_{1}
соответственно параллельны сторонам ортотреугольника треугольника ABC
(см. задачу 700).
б) Докажем, что точка A_{2}
делит (внешним образом) сторону BC
на отрезки, пропорциональные квадратам сторон AB
и AC
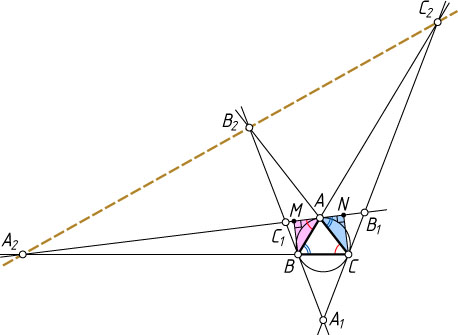
. Рассмотрим случай, изображённый на рисунке.
Пусть M
и N
— проекции точек соответственно B
и C
на прямую B_{1}C_{1}
. Тогда
\frac{BA_{2}}{A_{2}C}=\frac{BM}{CN}=\frac{AB\sin\angle A_{2}AB}{AC\sin\angle CAB_{1}}=\frac{AB}{AC}\cdot\frac{\sin\angle ACB}{\sin\angle ABC}=\frac{AB}{AC}\cdot\frac{AB}{AC}=\frac{AB^{2}}{AC^{2}}.
Что и требовалось доказать.
Аналогично для точек B_{2}
и C_{2}
. Тогда
\frac{AB_{2}}{B_{2}C}\cdot\frac{CA_{2}}{A_{2}B}\cdot\frac{BC_{2}}{C_{2}A}=\frac{AB^{2}}{BC^{2}}\cdot\frac{AC^{2}}{AB^{2}}\cdot\frac{BC^{2}}{AC^{2}}=1.
Следовательно, по теореме Менелая (см. задачу 1622) точки A_{2}
, B_{2}
и C_{2}
лежат на одной прямой.
Аналогично для любого другого случая.
в) См. задачу 178.
Примечание. 1. Треугольник A_{1}B_{1}C_{1}
, образованный касательными к описанной окружности треугольника ABC
, проведёнными в точках касания, называется тангенциальным треугольником треугольника ABC
.
2. Также можно воспользоваться теоремой Паскаля для вырожденного шестиугольника AABBCC
(см. 6390).
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 148
