10878. Пусть высоты AA_{1}
, BB_{1}
и CC_{1}
остроугольного неравнобедренного треугольника ABC
пересекаются в точке H
, M
— середина стороны AB
, а касательные, проведённые в точках A
и B
к описанной окружности треугольника ABC
, пересекаются в точке Z
. Докажите, что прямые MH
, A_{1}B_{1}
и ZC_{1}
пересекаются в одной точке.
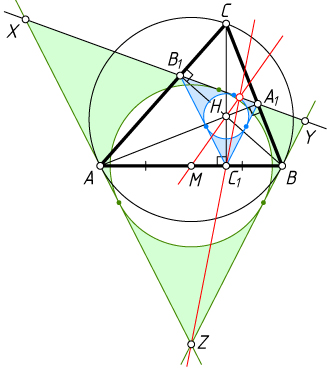
Решение. Пусть касательные к описанной окружности треугольника ABC
в точках A
и B
пересекают прямую A_{1}B_{1}
в точках X
и Y
соответственно. Стороны C_{1}B_{1}
и C_{1}A_{1}
треугольника A_{1}B_{1}C_{1}
соответственно параллельны сторонам ZX
и ZY
треугольника YXZ
(см. задачу 700), а сторона A_{1}B_{1}
лежит на стороне XY
, значит, эти треугольники гомотетичны (см. задачу 5000), причём центр гомотетии лежит на прямой XY
. При этой гомотетии вершина C_{1}
треугольника A_{1}B_{1}C_{1}
соответствует вершине Z
треугольника YXZ
, а центр H
вписанной окружности треугольника A_{1}B_{1}C_{1}
(см. задачу 533) — центру M
вписанной окружности треугольника YXZ
(см. задачу 10876). Значит, прямые ZC_{1}
и MH
пересекаются в центре гомотетии, т. е. в точке, лежащей на прямой A_{1}B_{1}
. Следовательно, прямые MH
, A_{1}B_{1}
и ZC_{1}
пересекаются в одной точке.
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Блинков Ю. А.
Источник: Журнал «Квант». — 2014, № 1, с. 45
