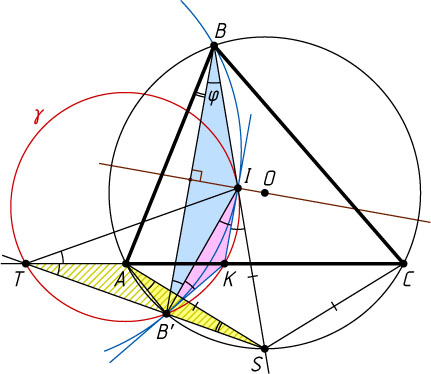
13354. Неравнобедренный треугольник ABC
вписан в окружность с центром O
и описан около окружности с центром I
. Точка B'
, симметричная точке B
относительно прямой OI
, лежит внутри угла ABI
. Докажите, что касательные к окружности, описанной около треугольника BB'I
, проведённые в точках B'
и I
, пересекаются на прямой AC
.
Решение. Первый способ. Пусть прямая BI
вторично пересекает окружность, описанную около треугольника ABC
, в точке S
, а лучи SB'
и CA
пересекаются в точке T
(рис. 1). По теореме о трилистнике SA=SC=SI
(см. задачу 788). Обозначим \angle IB'B=\angle IBB'=\varphi
. Окружность симметрична относительно любого своего диаметра (см. задачу 1677), поэтому точка B'
лежит на описанной окружности треугольника ABC
. Тогда
\angle SAB'=\angle SBB'=\varphi.
Угол SAC
— внешний для треугольника SAT
, поэтому
\angle ATS=\angle SAC-\angle ASB'=\angle SBC-\angle ABB'=
=\angle SBA-\angle ABB'=\angle SBB'=\varphi.
Таким образом,
\angle B'AS=\varphi=\angle ATS,
значит, треугольники SAB'
и STA
подобны по двум углам, поэтому
\frac{SB'}{SA}=\frac{SA}{ST}~\Rightarrow~SB'\cdot ST=SA^{2}=SI^{2}.
Следовательно, прямая SI
касается окружности \gamma
, описанной около треугольника TIB'
(см. задачу 4776). Тогда \angle ITB'=\angle B'IS
(см. задачу 87), а так как B'IS
— внешний угол треугольника IBB'
, то \angle B'IS=2\varphi
. Значит,
\angle ITA=\angle ITB'-\angle ATB'=2\varphi-\varphi=\varphi.
Обозначим вторую точку пересечения окружности \gamma
с прямой AC
через K
. Поскольку TK
— биссектриса вписанного угла ITB'
, то
\angle KIB'=\angle KB'I=\angle KTI=\varphi=\angle IB'B,
\angle IB'K=\angle KIB'=\varphi=\angle IBB'.
Таким образом (см. задачу 144), прямые KI
и KB'
касаются окружности, описанной около треугольника BB'I
, а точка K
лежит на прямой AC
по построению.
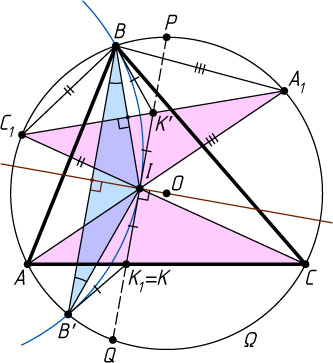
Второй способ. Поскольку OB=OB'
из симметрии, точка B'
лежит на окружности \Omega
, описанной около треугольника ABC
. Пусть лучи AI
и CI
вторично пересекают окружность \Omega
в точках A_{1}
и C_{1}
соответственно, а K
— точка пересечения касательных к окружности, описанной около треугольника BB'I
, проведённых в точках B'
и I
. Тогда KI=KB'
.
Поскольку IB'=IB
, то
\angle IB'B=\angle IBB'=\angle KIB',
поэтому KI\parallel BB'
и KI\perp OI
.
Пусть K'
— точка, симметричная точке K
относительно прямой OI
, а K_{1}
— точка пересечения прямых KI
и AC
(рис. 2). Поскольку KB'=KI
, из симметрии получаем, что K'B=KI=K'I
. Кроме того, C_{1}B=C_{1}I
и A_{1}B=A_{1}I
по теореме о трилистнике (см. задачу 788). Таким образом, точки K'
, A_{1}
и C_{1}
лежат на одной прямой — серединном перпендикуляре к отрезку BI
.
Пусть прямая IK
пересекает окружность \Omega
в точках P
и Q
. Поскольку OI\perp PQ
, по теореме о бабочке для хорд AA_{1}
и CC_{1}
, проходящих через середину I
хорды PQ
(см. задачу 122), получаем, что K'I=IK_{1}
, а так как из симметрии K'I=IK
, то точки K_{1}
и K
совпадают. Отсюда следует утверждение задачи.
Автор: Кузнецов А. С.
Источник: Всероссийская олимпиада школьников. — 2016-2017, XLIII, заключительный этап, второй день, задача 8, 10 класс

