13705. Четырёхугольник ABCD
вписан в окружность. Прямые AB
и DC
пересекаются в точке P
, а прямые AD
и BC
— в точке Q
. Прямые, проходящее через точку Q
, касаются окружности в точках E
и F
. Докажите, что точки P
, E
и F
лежат на одной прямой.
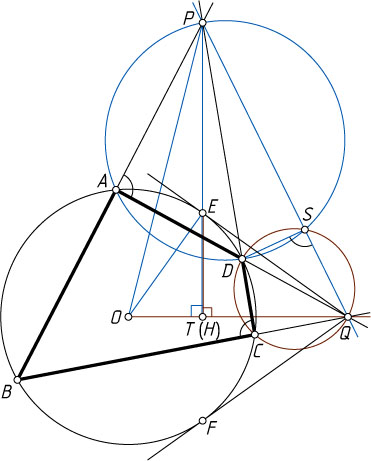
Решение. Рассмотрим случай, изображённый на рисунке. Пусть O
и R
— центр и радиус описанной окружности четырёхугольника ABCD
, а S
— отличная от P
точка пересечения прямой PQ
с описанной окружностью треугольника PAD
. Тогда
\angle DSQ=\angle PAD=\angle DCB,
поэтому точки C
, D
, S
, Q
лежат на одной окружности. Значит (см. задачи 2623 и 2636),
PS\cdot PQ=PD\cdot PC=PO^{2}-R^{2}.
Аналогично,
QS\cdot PQ=QD\cdot QA=QO^{2}-R^{2}.
Следовательно,
PQ^{2}=(PS+SQ)\cdot PQ=PS\cdot PQ+QS\cdot PQ=
=(PO^{2}-R^{2})+(QO^{2}-R^{2})=PO^{2}+QO^{2}-2R^{2}.
С другой стороны, по теореме косинусов
PQ^{2}=PO^{2}+QO^{2}-2PO\cdot PQ\cos\angle POQ.
Из равенства
PO^{2}+QO^{2}-2R^{2}=PO^{2}+QO^{2}-2PO\cdot PQ\cos\angle POQ
находим, что
R^{2}=PO\cdot QO\cos\angle POQ.
Пусть T
— проекция точки P
на прямую OQ
. Тогда
OT=PO\cos\angle POQ=\frac{R^{2}}{QO}.
Пусть H
— проекция точки E
на прямую OQ
. Тогда из прямоугольного треугольника OEQ
получаем (см. задачу 2728)
OH=\frac{OE^{2}}{OQ}=\frac{R^{2}}{QO}
Из равенства OH=OT
следует, что точки H
и T
совпадают.
Поскольку PT\perp OQ
и EH\perp OQ
, то прямая PT
совпадает с прямой EH
, т. е. с прямой EF
(см. задачу 1180). Таким образом, точки P
, E
и F
лежат на одной прямой. Что и требовалось доказать.
Аналогично для любого другого случая.
Примечание. См. также задачу 1088.
Источник: Журнал «Crux Mathematicorum». — 2002, № 6, задача 4, с. 358
Источник: Китайские математические олимпиады. — 1997
