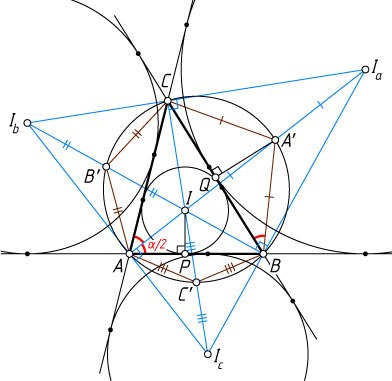
16036. В треугольник ABC
вписана окружность с центром I
. Лучи AI
, BI
и CI
пересекают описанную окружность треугольника в точках A'
, B'
и C'
соответственно. Докажите что
0\leqslant IA'+IB'+IC'-(IA+IB+IC)\leqslant3(R-2r),
где R
и r
— радиусы соответственно описанной и вписанной окружностей треугольника ABC
.
Решение. Пусть углы треугольника ABC
, противолежащие сторонам BC=a
, CA=b
и AB=c
, равны \alpha
, \beta
и \gamma
соответственно, I_{a}
, I_{b}
и I_{c}
— центры вневписанных окружностей треугольника ABC
, касающихся сторон BC
, CA
и AB
соответственно. Тогда IA\perp I_{b}I_{c}
, IB\perp I_{a}I_{c}
и IC\perp I_{a}I_{b}
(см. задачу 4769). Применив к треугольнику I_{a}I_{b}I_{c}
неравенство Эрдёша—Морделла (см. задачу 11263б), получим
II_{a}+II_{b}+II_{c}\geqslant2(IA+IB+IC),
а так как по теореме Мансиона (см. задачу 57)
II_{a}=2IA',~II_{b}=2IB',~II_{c}=2IC',
то
(IA'-IA)+(IB'-IB)+(IC'-IC)\geqslant0.
Далее см. задачи 4947 и 4941б.
Примечание. Верно более сильное неравенство
0\leqslant IA'+IB'+IC'-(IA+IB+IC)\leqslant2(R-2r)
(оригинальное условие из источника).
Источник: Журнал «Crux Mathematicorum». — 1988, № 10, задача 1282 (1987, с. 289), с. 305
