16185. Биссектрисы треугольника ABC
, проведённые из вершин A
, B
и C
, пересекают описанную окружность треугольника в точках A'
, B'
и C'
соответственно. Прямая A'B'
пересекает стороны BC
и AC
в точках P
и Q
соответственно, прямая B'C'
пересекает стороны AC
и AB
в точках R
и S
соответственно, прямая C'A'
пересекает стороны AB
и BC
в точках P
и Q
соответственно. Докажите, что отношение площадей шестиугольника PQRSTU
и треугольника ABC
равно
\frac{S_{PQRSTU}}{S_{\triangle ABC}}=\frac{(a+b)^{2}+(b+c)^{2}+(c+a)^{2}}{2(a+b+c)^{2}}.
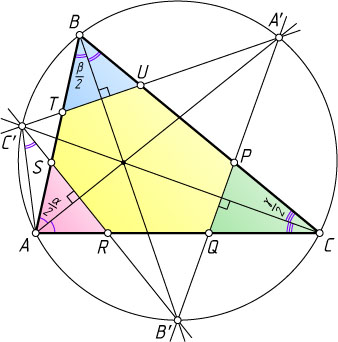
Решение. Рассмотрим случай, изображённый на рисунке.
Обозначим углы треугольника ABC
, противолежащие сторонам BC=a
, CA=b
и AB=c
, через \alpha
, \beta
и \gamma
соответственно, p
— полупериметр треугольника, d
— диаметр описанной окружности, s
и s_{1}
— площади треугольника ABC
и шестиугольника PQRSTU
.
Биссектрисы треугольника ABC
содержат высоты треугольника A'B'C'
(см. задачу 33), поэтому треугольники ARS
, TBU
и PCQ
равнобедренные с основаниями RS
, TU
и PQ
соответственно.
Поскольку
\angle AC'R=\angle AC'B'=\angle ABB'=\frac{\beta}{2}~\mbox{и}~\angle ARC'=\angle ARS=\angle ASR=90^{\circ}-\frac{\alpha}{2},
то по теореме синусов из треугольника AC'R
получаем
\frac{AR}{\sin\frac{\beta}{2}}=\frac{AC'}{\sin\left(90^{\circ}-\frac{\alpha}{2}\right)}=\frac{AC'}{\cos\frac{\alpha}{2}},
откуда (см. задачу 23)
AS=AR=\frac{AC'\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}}=\frac{d\sin\angle ACC'\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}}=\frac{d\sin\frac{\gamma}{2}\sin\frac{\beta}{2}}{\cos\frac{\alpha}{2}}.
Тогда (см. задачу 3007)
\frac{S_{\triangle ARS}}{s}=\frac{AS}{AB}\cdot\frac{AR}{AC}=\frac{AS}{c}\cdot\frac{AR}{b}=\frac{d^{2}\sin^{2}\frac{\beta}{2}\sin^{2}\frac{\gamma}{2}}{bc\cos^{2}\frac{\alpha}{2}}.
Заметим, что
\cos^{2}\frac{\alpha}{2}=\frac{1}{2}(1+\cos\alpha)=\frac{1}{2}\left(1+\frac{b^{2}+c^{2}-a^{2}}{2bc}\right)=\frac{1}{2}\cdot\frac{2bc+b^{2}+c^{2}-a^{2}}{2bc}=
=\frac{(b+c)^{2}-a^{2}}{4bc}=\frac{(a+b+c)(b+c-a)}{4bc}=\frac{p(p-a)}{bc},
\sin^{2}\frac{\alpha}{2}=\frac{1}{2}(1-\cos\alpha)=\frac{1}{2}\left(1-\frac{b^{2}+c^{2}-a^{2}}{2bc}\right)=\frac{1}{2}\cdot\frac{2bc-b^{2}-c^{2}+a^{2}}{2bc}=
=\frac{a^{2}-(b-c)^{2}}{4bc}=\frac{(a-b+c)(a+b-c)}{4bc}=\frac{(p-b)(p-c)}{bc}.
Аналогично,
\sin^{2}\frac{\gamma}{2}=\frac{(p-a)(p-b)}{ab}~\sin^{2}\frac{\beta}{2}=\frac{(p-a)(p-c)}{ac}.
Значит (см. задачи 2730 и 4259),
\frac{S_{\triangle ARS}}{s}=\frac{d^{2}\sin^{2}\frac{\beta}{2}\sin^{2}\frac{\gamma}{2}}{bc\cos^{2}\frac{\alpha}{2}}=\frac{d^{2}}{p(p-a)}\cdot\frac{(p-a)(p-c)}{ac}\cdot\frac{(p-a)(p-b)}{ab}=
=\frac{d^{2}(p-a)(p-b)(p-c)}{pa^{2}bc}=\frac{d^{2}p(p-a)(p-b)(p-c)}{p^{2}a^{2}bc}=\frac{d^{2}s^{2}}{p^{2}a^{2}bc}=
=\frac{d^{2}\cdot\frac{a^{2}b^{2}c^{2}}{4d^{2}}}{p^{2}a^{2}bc}=\frac{bc}{4p^{2}}.
Аналогично,
\frac{S_{\triangle BTU}}{s}=\frac{ac}{4p^{2}},~\frac{S_{\triangle CPQ}}{s}=\frac{ab}{4p^{2}}.
Следовательно,
\frac{S_{PQRSTU}}{S_{\triangle ABC}}=\frac{s_{1}}{s}=\frac{s-S_{\triangle ARS}-S_{\triangle BTU}-S_{\triangle CPQ}}{s}=1-\frac{bc}{4p^{2}}-\frac{ac}{4p^{2}}-\frac{ab}{4p^{2}}=
=\frac{4p^{2}-bc-ac-ab}{4p^{2}}=\frac{(a+b+c)^{2}-bc-ac-ab}{(a+b+c)^{2}}=\frac{a^{2}+b^{2}+c^{2}+bc+ac+ab}{(a+b+c)^{2}}=
=\frac{2a^{2}+2b^{2}+2c^{2}+2bc+2ac+2ab}{2(a+b+c)^{2}}=\frac{(a+b)^{2}+(b+c)^{2}+(c+a)^{2}}{2(a+b+c)^{2}}.
Что и требовалось доказать.
Аналогично для любого другого случая.
Источник: Журнал «Crux Mathematicorum». — 2002, № 4, задача A249, с. 231
