16408. Даны концентрические окружности \Gamma_{1}
и \Gamma_{2}
с центром O
(радиус второй меньше радиуса первой). Постройте окружность \Gamma
с центром на \Gamma_{2}
, удовлетворяющую условию: касательные к окружности \Gamma
, проведённые из любой точки P
окружности \Gamma_{1}
, вторично пересекают окружность \Gamma_{1}
в таких точках Q
и S
, что прямая QS
касается окружности \Gamma
.
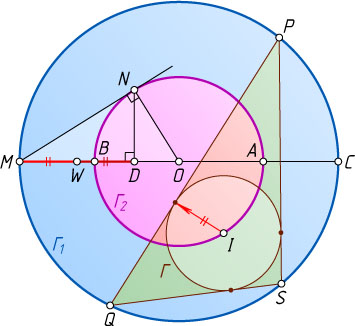
Решение. Предположим, такая окружность \Gamma
построена (см. рис.). Пусть I
— её центр, r
— радиус, R
— радиус окружности \Gamma_{1}
, MC
— диаметр окружности \Gamma_{1}
, Q
и S
— точки пересечения касательных, проведённых из точки P
окружности \Gamma_{1}
к окружности \Gamma
, OI=d
.
Тогда d
— расстояние между центрами O
и I
описанной и вписанной окружностей треугольника PQS
. По формуле Эйлера (см. задачу 126)
OI^{2}=d^{2}=R^{2}-2Rr.
Пусть прямая, проведённая через точку M
, касается окружности \Gamma_{2}
в точке N
, диаметр MC
пересекает окружность \Gamma_{2}
в точках A
и B
(B
между M
и O
), а ND
— высота прямоугольного треугольника MON
, проведённая из вершины прямого угла. Тогда по теореме о касательной и секущей MN^{2}=MA\cdot MB
(см. задачу 93), а ND^{2}=OD\cdot MD
(см. задачу 2728). Значит,
r=\frac{R^{2}-d^{2}}{2R}=\frac{(R-d)(R+d)}{2R}=\frac{(OM-OB)(OM+OB)}{2OM}=
=\frac{MB\cdot MA}{2OM}=\frac{MN^{2}}{2OM}=\frac{OM^{2}-ON^{2}}{2OM}=\frac{OM^{2}-(ND^{2}+OD^{2})}{2OM}=
=\frac{OM^{2}-(OD\cdot MD+OD^{2})}{2OM}=\frac{OM^{2}-OD(MD+OD)}{2OM}=\frac{OM^{2}-OD\cdot OM}{2OM}=
=\frac{1}{2}(OM-OD)=\frac{1}{2}DM=DW,
где W
— середина отрезка DM
.
Отсюда вытекает следующее построение. Проводим диаметр MC
данной окружности \Gamma_{1}
. Строим касательную MN
из точки M
к окружности \Gamma_{2}
, где N
— точка касания (см. задачу 1738). Проводим высоту ND
из вершины прямого угла треугольника MON
. Строим середину W
отрезка DM
, и радиусом r=DW
проводим окружность \Gamma
с центром в произвольной точке I
окружности \Gamma_{2}
.
Пусть касательные к построенной окружности, проведённые из произвольной точки P
окружности \Gamma_{1}
, пересекают окружность \Gamma_{1}
в точках Q
и S
. Предположим, что прямая QS
не касается окружности \Gamma
. Проведём касательную к \Gamma_{1}
, параллельную QS
и не пересекающую \Gamma_{2}
. Пусть она пересекает лучи PQ
и PS
в точках Q'
и S'
соответственно. Радиус вписанной окружности треугольника PQ'S'
не равен r
, значит, и расстояние между центрами описанной и вписанной окружностей не равно d=\sqrt{R^{2}-2Rr}
. Противоречие.
Следовательно, построенная окружность \Gamma
удовлетворяет условию задачи.
Источник: Журнал «Mathematics Magazine». — 1935, том 9, № 8, задача 84, с. 254
