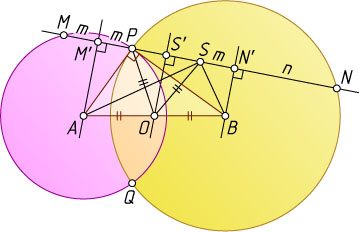
16445. Ортогональные окружности с центрами A
и B
пересекаются в точках P
и Q
. Прямая, проходящая через точку P
, пересекает эти окружности в точках M
и N
соответственно, S
— середина отрезка MN
. Докажите, что окружности девяти точек треугольников ABP
и ABS
равны.
Решение. Без ограничения общности рассмотрим случай, изображённый на рисунке.
Первый способ. Пусть M'
, N'
и S'
— середины отрезков PM
, PN
и PS
соответственно. Обозначим MM'=M'P=m
и PN'=N'N=n
. Тогда
2m+2n=MN~\Rightarrow~\frac{1}{2}MN=m+n.
Тогда
SN'=SN-NN'=\frac{1}{2}MN-n=m+n-n=m=M'N,
а так как PS'=S'S
, то S'
— середина отрезка M'N'
.
Поскольку AM'\perp MN
и BN'\perp MN
(см. задачу 1677), то по теореме Фалеса точка O
пересечения серединного перпендикуляра к MN
с прямой AB
— середина отрезка AB
. Значит, OP=OS
, а так как из ортогональности окружностей AP\perp BP
следует, что \angle APB=90^{\circ}
, то
OS=OP=\frac{1}{2}AB
(см. задачу 1109). Значит, треугольник ASB
тоже прямоугольный с прямым углом при вершине S
(см. задачу 1188).
Окружности девяти точек прямоугольных треугольников ABP
и ABS
— это окружности, диаметры которых — медианы соответственно OP
и OS
этих треугольников, проведённые из вершин прямых углов (см. задачу 174), а так как OP=OS
, то радиусы этих окружностей равны. Отсюда следует утверждение задачи.
Второй способ. Множество середин S
всевозможных отрезков MN
— окружность \Omega
, проходящая через точки P
и Q
(см. задачу 2491). Данные окружности ортогональны, поэтому частным случаем отрезка MN
является диаметр PA'
окружности с центром A
. Следовательно, окружность \Omega
проходит через A
. Аналогично, \Omega
проходит через B
. Треугольники ABS
и ABP
вписаны в одну и ту же окружность \Omega
, значит, их окружности девяти точек имеют равные радиусы, т. е. равны.
Источник: Журнал «Mathematics Magazine». — 1956, том 29, № 5, задача 255, с. 288
