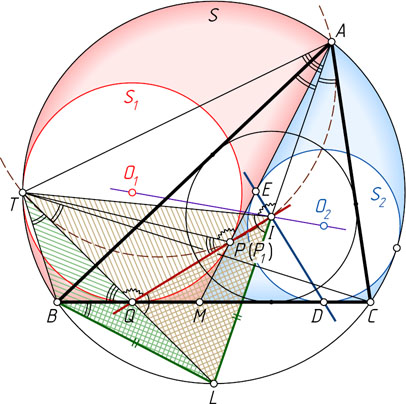
5076. Теорема Тебо. Окружность описана около треугольника ABC
. Точка M
лежит на стороне BC
. Докажите, что линия центров окружностей, вписанных в криволинейные треугольники AMB
и AMC
, проходит через центр вписанной окружности треугольника ABC
.
Решение. Пусть окружность S_{1}
, вписанная в криволинейный треугольник AMB
, касается отрезков AM
и BM
в точках P
и Q
соответственно, а описанной окружности S
треугольника ABC
— в точке T
. Соединим точку Q
с центром I
вписанной окружности треугольника ABC
. Докажем, что прямая QI
проходит через точку P
.
Предположим, что прямая QI
вторично пересекает окружность, вписанную в криволинейный треугольник AMB
, в точке P_{1}
.
Окружности S_{1}
и S
касаются внутренним образом. Хорда BC
окружности S
касается окружности S_{1}
в точке Q
. Значит, TQ
— биссектриса угла BTC
(см. задачу 89). Следовательно, луч TQ
пересекает окружность S
в середине L
дуги BC
, не содержащей точки A
. Точка I
лежит на биссектрисе вписанного в окружность S
угла BAC
, значит, прямая AI
также проходит через точку L
.
Угол между пересекающимися хордами TL
и BC
окружности S
равен полусумме противоположных дуг BT
и CL
(см. задачу 26), а L
— середина дуги BC
, поэтому
\angle TQB=\frac{1}{2}(\smile BT+\smile CL)=\frac{1}{2}(\smile BT+\smile BL)=
=\frac{1}{2}\smile TBL=\angle TAL=\angle TAI.
С другой стороны, из теоремы об угле между касательной и хордой следует, что \angle TQB=\angle TP_{1}Q
, поэтому либо
\angle TAI=\angle TP_{1}Q=180^{\circ}-\angle IP_{1}T,
либо
\angle TAI=\angle TP_{1}Q=\angle IP_{1}T,
а точки A
, I
, P_{1}
, T
лежат на одной окружности в каждом из этих случаев Значит, \angle AIT=\angle AP_{1}T
.
Вписанные в окружность S
углы BTL
и CBL
опираются на равные дуги, поэтому
\angle BTL=\angle CBL=\angle QBL.
Значит, треугольник QBL
подобен треугольнику BTL
по двум углам, поэтому \frac{BL}{TL}=\frac{QL}{BL}
. Тогда BL^{2}=QL\cdot TL
, а так как BL=IL
(см. задачу 788), то
IL^{2}=BL^{2}=QL\cdot TL.
Значит, \frac{IL}{QL}=\frac{TL}{IL}
, поэтому треугольник ILQ
подобен треугольнику TLI
по двум сторонам и углу между ними. Следовательно,
\angle IQL=\angle TIL=180^{\circ}-\angle AIT=180^{\circ}-\angle AP_{1}T.
В то же время,
\angle IQL=180^{\circ}-\angle IQT=180^{\circ}-\angle P_{1}QT,
значит, \angle AP_{1}T=\angle P_{1}QT
. Следовательно, AP_{1}
— касательная к окружности S_{1}
(см. задачу 144), и точка P_{1}
совпадает с P
. Таким образом доказано, что прямая PQ
проходит через точку I
.
Пусть O_{1}
— центр окружности S_{1}
, а O_{2}
— центр окружности S_{2}
, вписанной в криволинейный треугольник AMC
и касающейся отрезка BC
в точке D
, а отрезка AM
— в точке E
. Тогда DQ
— общая внешняя касательная окружностей S_{1}
и S_{2}
, а EP
— их общая внутренняя касательная. Прямые DE
и PQ
пересекаются на линии центров O_{1}O_{2}
этих окружностей (см. задачу 1083). С другой стороны, по доказанному, обе эти прямые проходят через точку I
. Отсюда следует доказательство теоремы.
Примечание. См. статью В.Протасова «Касающиеся окружности: от Тебо до Фейербаха», Квант, 2008, N4, с.10.
Источник: Журнал «Квант». — 2008, № 4, с. 10
