5448. На отрезке AC
взята точка B
, отличная от A
и C
. Рассматриваются всевозможные окружности S
, проходящие через точки A
и B
. Из точки C
к каждой из таких окружностей проводится по две касательные; обозначим K
и L
точки касания. Найдите геометрическое место середин отрезков KL
.
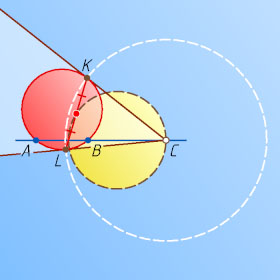
Ответ. Окружность без точки.
Указание. Пусть M
— середина KL
, X
— точка пересечения отрезков KL
и AB
. Докажите, что CX=\frac{2CA\cdot CB}{CB+CA}
. (см. задачи 2728, 93, 4776).
Решение. Пусть M
— середина KL
, X
— точка пересечения отрезков KL
и AB
, H
— проекция центра O
окружности на хорду AB
.
Тогда OC\perp KM
; H
— середина AB
, поэтому CH=\frac{1}{2}(CA+CB)
; KM
— высота прямоугольного треугольника OKC
, проведённая из вершины прямого угла, поэтому CM\cdot CO=CK^{2}
(см. задачу 2728). По теореме о касательной и секущей CK^{2}=CA\cdot CB
(см. задачу 93).
Прямоугольные треугольники CMX
и CHO
подобны, поэтому \frac{CM}{CH}=\frac{CX}{CO}
, значит,
CX=\frac{CM\cdot CO}{CH}=\frac{CK^{2}}{\frac{1}{2}(CA+CB)}=\frac{CA\cdot CB}{\frac{1}{2}(CA+CB)}=\frac{2CA\cdot CB}{CA+CB}.
Следовательно, X
— фиксированная точка отрезка AB
.
Из каждой точки M
отрезок XC
виден под прямым углом, значит, точка M
лежит на окружности с диаметром XC
.
Пусть теперь M
— произвольная точка окружности с диаметром CX
, отличная от C
, где точка X
такова, что CX=\frac{2CA\cdot CB}{CA+CB}
. С центром в точке O
пересечения прямой CM
с серединным перпендикуляром к отрезку AB
построим окружность S
радиуса OA=OB
.
С центром в точке C
построим окружность радиуса \sqrt{CA\cdot CB}
. Пусть она пересекает окружность S
в точках K
и L
. Тогда CK
и CL
— касательные к окружности S
(см. задачу 4776). Докажем, что M
— середина KL
.
Действительно, аналогично предыдущему докажем, что точка Y
пересечения KL
и AC
удовлетворяет условию CY=\frac{2CA\cdot CB}{CA+CB}
, а так как точка X
— единственная такая точка, то Y
совпадает с X
. Кроме того, KL\perp OM
, следовательно, M
— середина KL
. Что и требовалось доказать.
Таким образом, искомое геометрическое место точек есть окружность с диаметром CX
без точки C
.
Примечание. Окружность с диаметром CX
— это одна из окружностей Аполлония отрезка AB
(см. задачу 2444).
Источник: Олимпиада «Физтех» (математическая олимпиада МФТИ). — 2000, 14-я заочная физ.-мат. олимпиада ФМБФ для школьников
